Найдите все углы треугольника, в особбености тот что выделен знаком вопроса

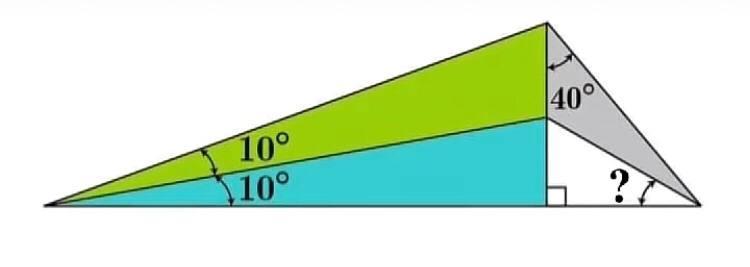
Ответ:

Для решения задачи найдем сначала два угла треугольника с помощью теоремы косинусов:

cos(A) = (b^2 + c^2 - a^2) / (2bc)

cos(B) = (a^2 + c^2 - b^2) / (2ac)

cos(A) = (3^2 + 5^2 - 4^2) / (235) = 22/30 = 11/15

A = arccos(11/15) ≈ 47.1°

cos(B) = (3^2 + 4^2 - 5^2) / (234) = 7/12

B = arccos(7/12) ≈ 54.2°

Третий угол находим, вычитая сумму первых двух углов из 180°:

C = 180° - A - B ≈ 78.7°

Треугольник остроугольный, так как все его углы меньше 90°. Угол, образованный боковой стороной и диагональю равенства, равен 180° - C, то есть приблизительно 101.3°.