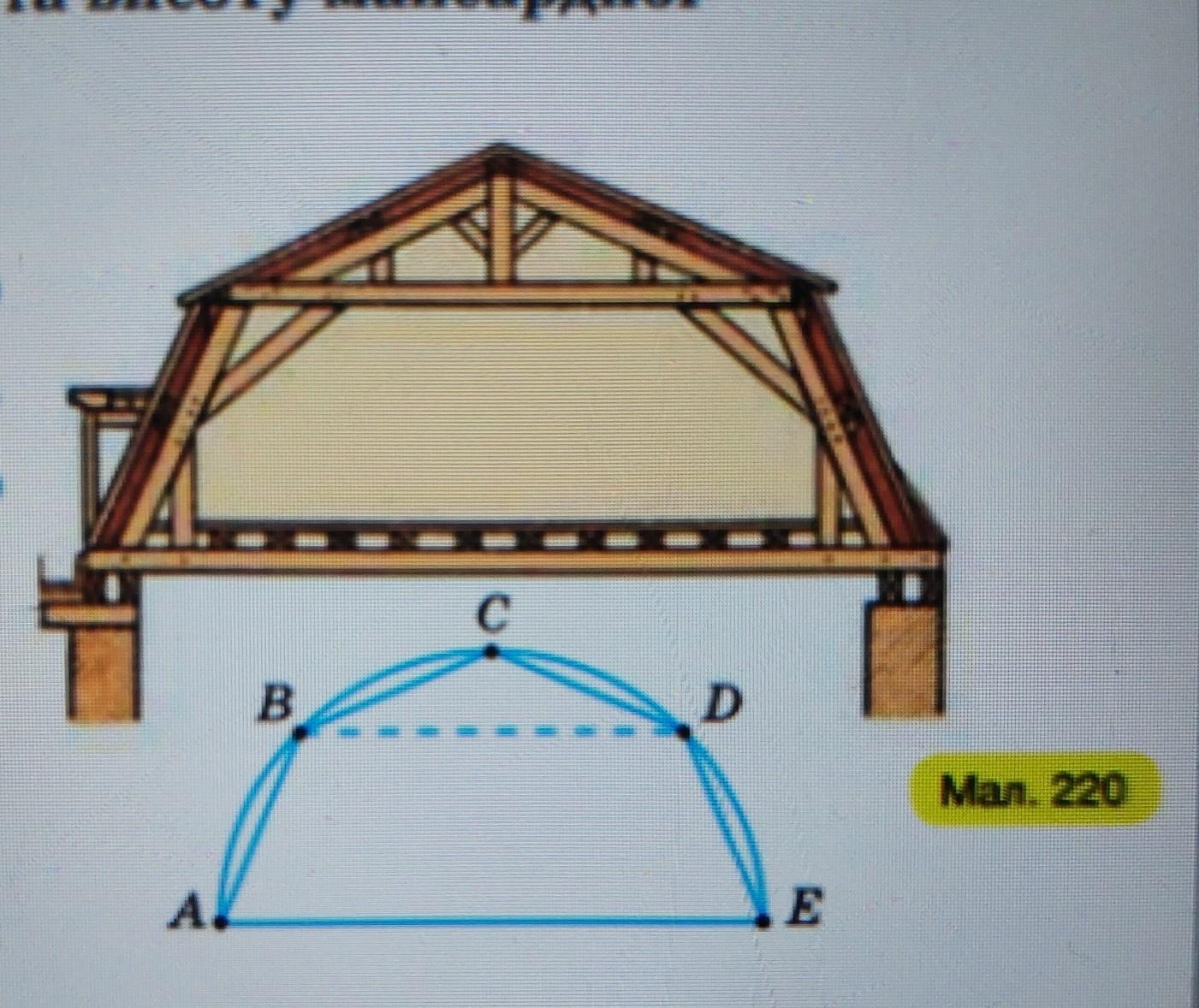
Найпростіше мансардне покриття утворює у вертикальному перерізі половину правильного восьмикутника (мал. 220). Знайдіть ширину перекриття BD, сторону восьмикутника та висоту мансардної кімнати ABCDE, якщо АЕ = 6 м.​

Ответ:

За умовою, перекриття утворює половину правильного восьмикутника. Оскільки восьмикутник - правильний, то кожен з його кутів дорівнює:

$$

\frac{360^\circ}{8} = 45^\circ

$$

За теоремою Піфагора у правильному восьмикутнику сторона в складі прямокутного трикутника може бути знайдена як:

$$

a = \frac{s}{\sqrt{2 - 2\cos 45^\circ }} = \frac{s}{\sqrt{2}}

$$

де $s$ - довжина сторони восьмикутника. Тому

$$

s = a\sqrt{2}

$$

За умовою, $AE = 6$ м. Позначимо через $h$ висоту прямокутної мансардної кімнати (від А до С). Тоді висота покриття (від С до B) також дорівнює $h$, а ширина перекриття відповідає стороні восьмикутника, тобто $s$. Тому маємо систему рівнянь:

$$

\begin{cases}

h + s = BD \\

h^2 + (s/2)^2 = 6^2

\end{cases}

$$

Розв'язуючи її, маємо:

$$

s = a\sqrt{2} = \frac{6}{\sqrt{8}} = \frac{3\sqrt{2}}{2} \approx 2.12 \text{ м}

$$

$$

h = \sqrt{6^2 - \left(\frac{s}{2}\right)^2} = \sqrt{36 - \frac{18}{4}} = \frac{3\sqrt{14}}{2} \approx 5.27 \text{ м}

$$

$$

BD = h + s \approx 7.39 \text{ м}

$$

Отже, ширина перекриття $BD \approx 7.39$ м, сторона восьмикутника $s \approx 2.12$ м, а висота мансардної кімнати $h \approx 5.27$ м.