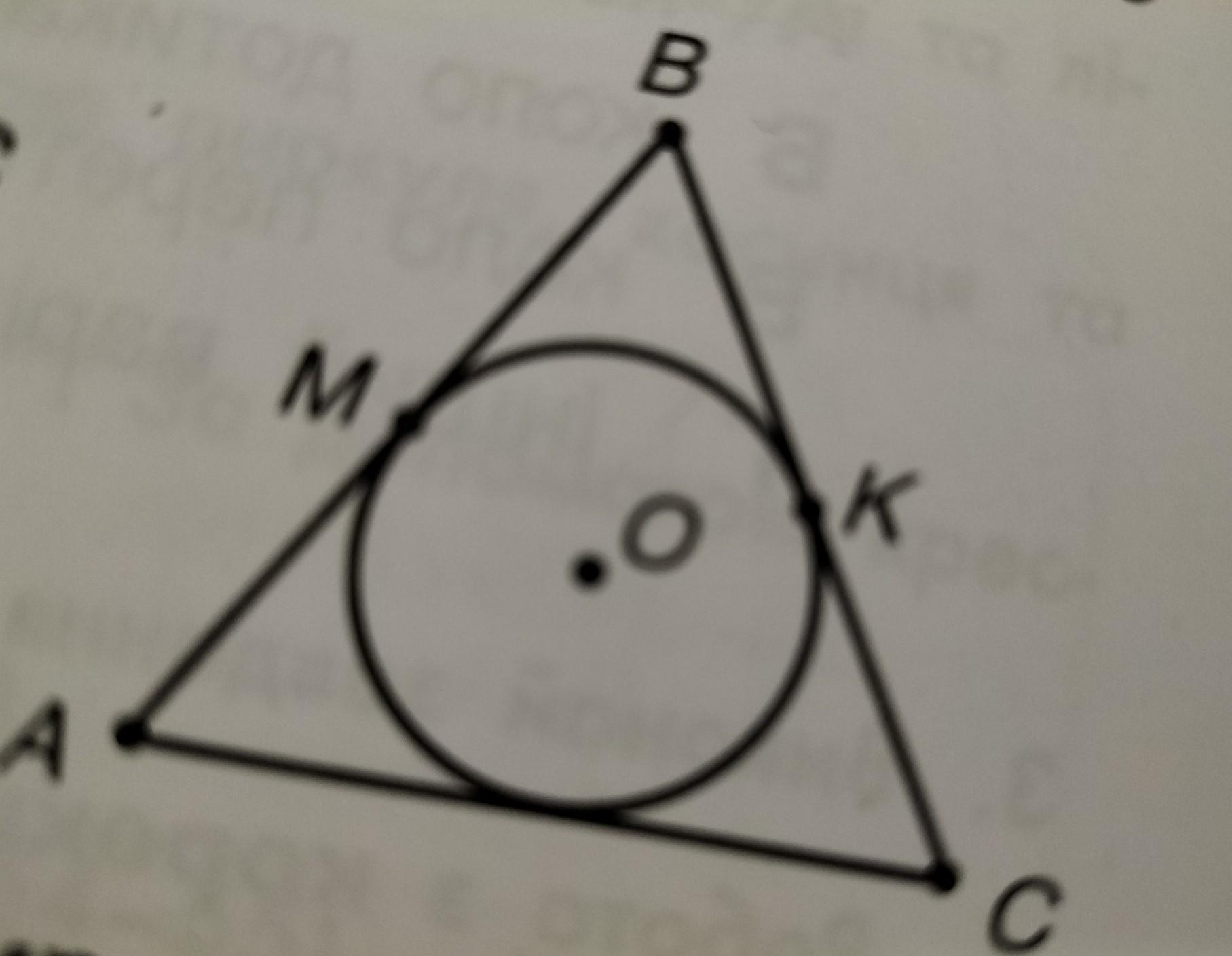
Дано AB = BC = 18 см, периметр трикутника ABC дорівнює 48 см. Точка О центр кола, вписаного в трикутник ABC. Обчисли довжину відрізків КС та BM. Допоможіть будь ласка!! ​

Позначимо довжину відрізка $AC$ через $x$. Оскільки $AB = BC$, то трикутник $ABC$ є ізоскелесним, тому $AM = MC = (48-18-x)/2 = (30-x)/2$.Так як точка $O$ є центром вписаного кола, то $OA = OB = OC = r$, де $r$ - радіус вписаного кола. Оскільки $AB = BC$, то кут $ABC$ дорівнює $120^\circ$. Позначимо кут $BAC$ через $\alpha$. Тоді кут $ACB$ також дорівнює $120^\circ$ і кут $ABC$ дорівнює $360^\circ - \alpha - 120^\circ - \alpha = 120^\circ - 2\alpha$. З іншого боку, кут $ABC$ можна знайти з косинусного правила:182=x2+(30−x)2−2x(30−x)cos⁡(120∘−2α).18 2 =x 2 +(30−x) 2 −2x(30−x)cos(120 ∘ −2α).Розв'язуючи це рівняння відносно $x$, отримуємо $x = 12 + 6\sqrt{3}\cos\alpha$. Тоді $AM = (30-x)/2 = 9 - 3\sqrt{3}\cos\alpha$ і радіус вписаного кола:r=Sp=3x212+33x=5412+33x,r= pS​ = 12+3 3​ x3​ x 2​ = 12+3 3​ x54​ ,де $S$ - площа трикутника $ABC$, а $p$ - його півпериметр.Тепер можна знайти довжину відрізка $BM$. Оскільки $BM$ є бісектрисою кута $ABC$, то відомо, що $BM$ ділить відрізок $AC$ у відношенні довжин $AB:BC$. ТомуBM=AB⋅ACAB+BC=(18)(x)36=x2.BM= AB+BCAB⋅AC​ = 36(18)(x)​ = 2x​ .Таким чином, $BM = 6+3\sqrt{3}\cos\alpha$.Для знаходження довжини відрізка $KC$ ми можемо скористатися теоремою Піфагора в прямокутному трикутнику $OMK$:OK2=OM2+MK2=r2+(x2)2,OK 2 =OM 2 +MK 2 =r 2 +( 2x​ ) 2 ,томуKC = 2\cdot OK = 2\sqrt{r^2 + \left(\frac{x}{2}\right)^2} = 6\sqrt{4+