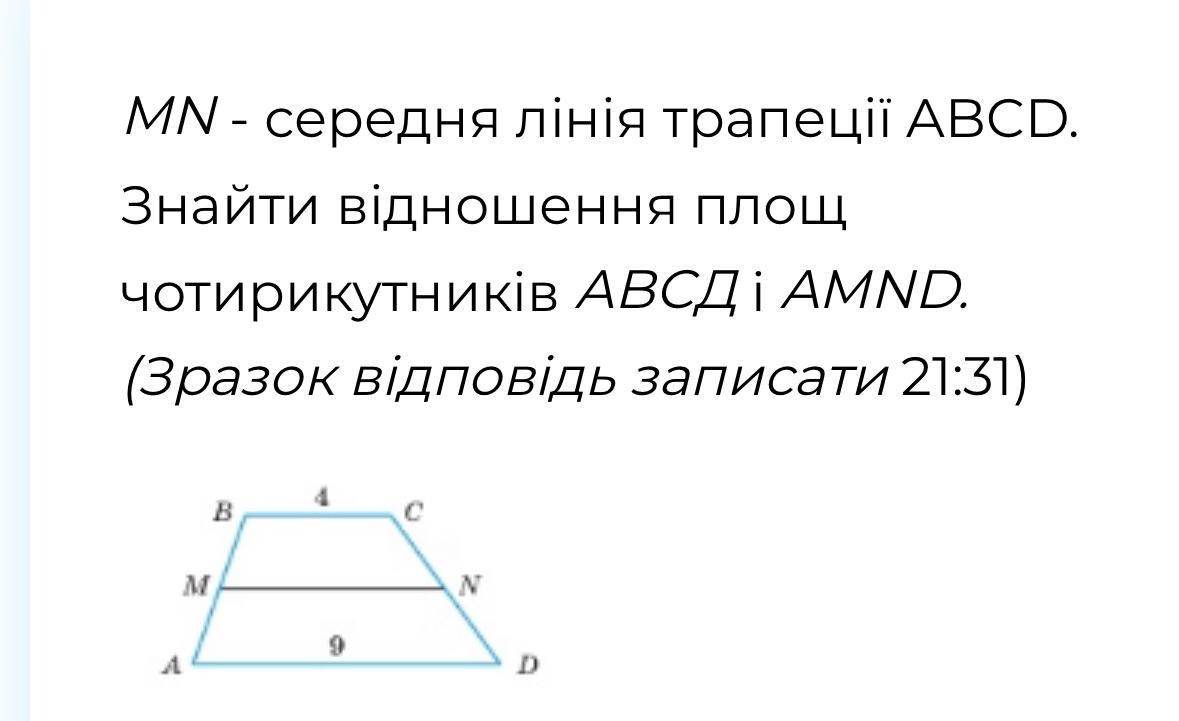
MN - середня лінія трапеції ABCD. Знайти відношення площ чотирикутників АBCД і AMND.

Спочатку знайдемо координати точок A, B, C і D. Нехай точка M має координати (х, у). Оскільки M є серединою сторони AD, то координати точок A і D мають вигляд:

A (2х, 2)

D (2х, 6)

Оскільки BC || AD і BM є діагоналлю трапеції, то координати точок B і C мають вигляд:

B (х + 2, 0)

C (х − 2, 0)

Точки B і C мають однакову ординату, тому вони лежать на одній горизонтальній прямій. Точки A і D також мають однакову ординату і лежать на іншій горизонтальній прямій паралельній першій. Таким чином, АВ || CD і BC || AD. Тому ABCD є трапецією.

Для знаходження площ кожної з фігур знайдемо їх базиси та висоти.

Базиси трапеції:

AB = CD = 4

BC = AD = 2 MN = 4

Висота трапеції:

h = BM = ND = у

За формулою площі трапеції, площа ABCD дорівнює:

S(ABCD) = ((AB+CD)*h)/2 = (4*(2у))/2 = 4y

Площу чотирикутника AMND можна розбити на два прямокутники зі сторонами AM і MN та DN і MN відповідно.

S1(AMND) = AM * MN

S2(AMND) = DN * MN

Оскільки AM = DN, то:

S(AMND) = S1(AMND) + S2(AMND) = AM*MN + DN*MN = 2AM*MN

Тому відношення площ буде:

S(ABCD) : S(AMND) = 4y : 2y = 2 : 1

Відповідь: відношення площ чотирикутників АBCД і AMND – 2 : 1.