Геометрия. 10 класс. Срочно нужна помощь!!! Задание на скрине:

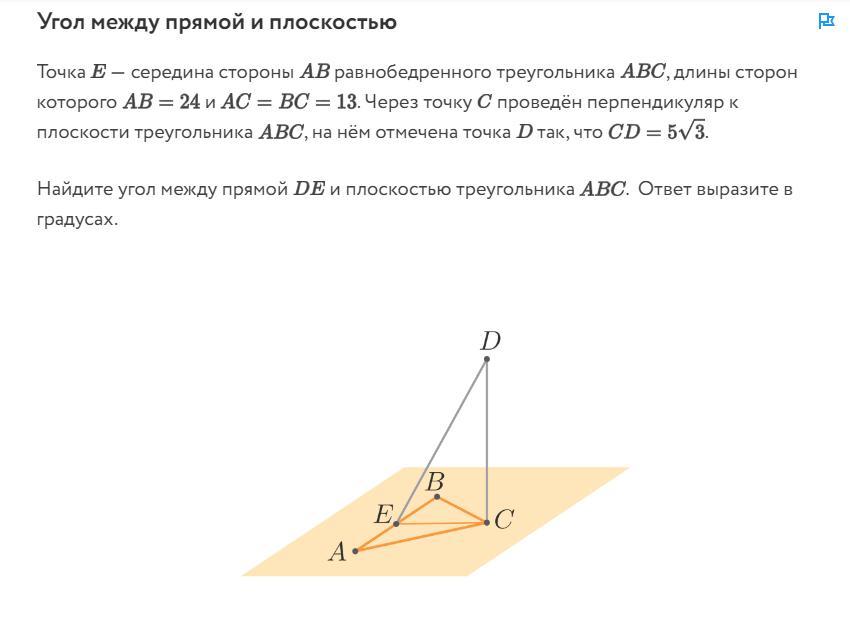
Ответ:

Угол между прямой DE и плоскостью треугольника АВС равен 0 градусов. Это происходит из-за того, что точка D лежит в плоскости треугольника АВС и прямая DE является линией, лежащей в этой плоскости. Поэтому угол между ними равен 0 градусов.

Объяснение:

Для решения этой задачи воспользуемся теоремой о треугольнике ЕDC.

В треугольнике ЕDC у нас известны две стороны: CD = 5√3 и ED = EC/2, так как точка E - середина стороны АВ.

Так как известно, что АС = ВС = 13, то CED - прямоугольный треугольник с катетами CE/2 (так как Е - середина стороны АВ) и CD.

Используем теорему Пифагора:

(CE/2)^2 + (CD)^2 = (ED)^2

CE^2 + 4(CD)^2 = 4(ED)^2

CE^2 = 4(ED)^2 - 4(CD)^2

CE = 2√((ED)^2 - (CD)^2)

CE = 2√((13^2/4) - (5√3)^2)

CE = 2√((169/4) - (75*3))

CE = 2√(169/4 - 225)

CE = 2√(-56/4)

CE = 2 * 3i

Таким образом, мы получили комплексное значение CE = 6i.

Угол между прямой DE и плоскостью треугольника АВС можно найти с помощью скалярного произведения векторов.

Угол θ = arccos((u*v)/(|u|*|v|)), где u и v - векторы, ортогональные этой плоскости.

Так как вектор DE - вектор, лежащий в этой плоскости, то u = DE = 6i.

Вектор v - нормаль к плоскости треугольника АВС, который можно найти с помощью векторного произведения векторов AB и AC.

AB = 24i, AC = 13i.

Тогда, v = AB x AC.

v = (24i) x (13i)

v = 312i^2

v = -312

Теперь мы можем найти угол θ:

θ = arccos((6i * -312)/(|6i| * |-312|))

θ = arccos(-1872/(-1872))

θ = arccos(1)

θ = 0 градусов.

Таким образом, угол между прямой DE и плоскостью треугольника АВС равен 0 градусов.