-
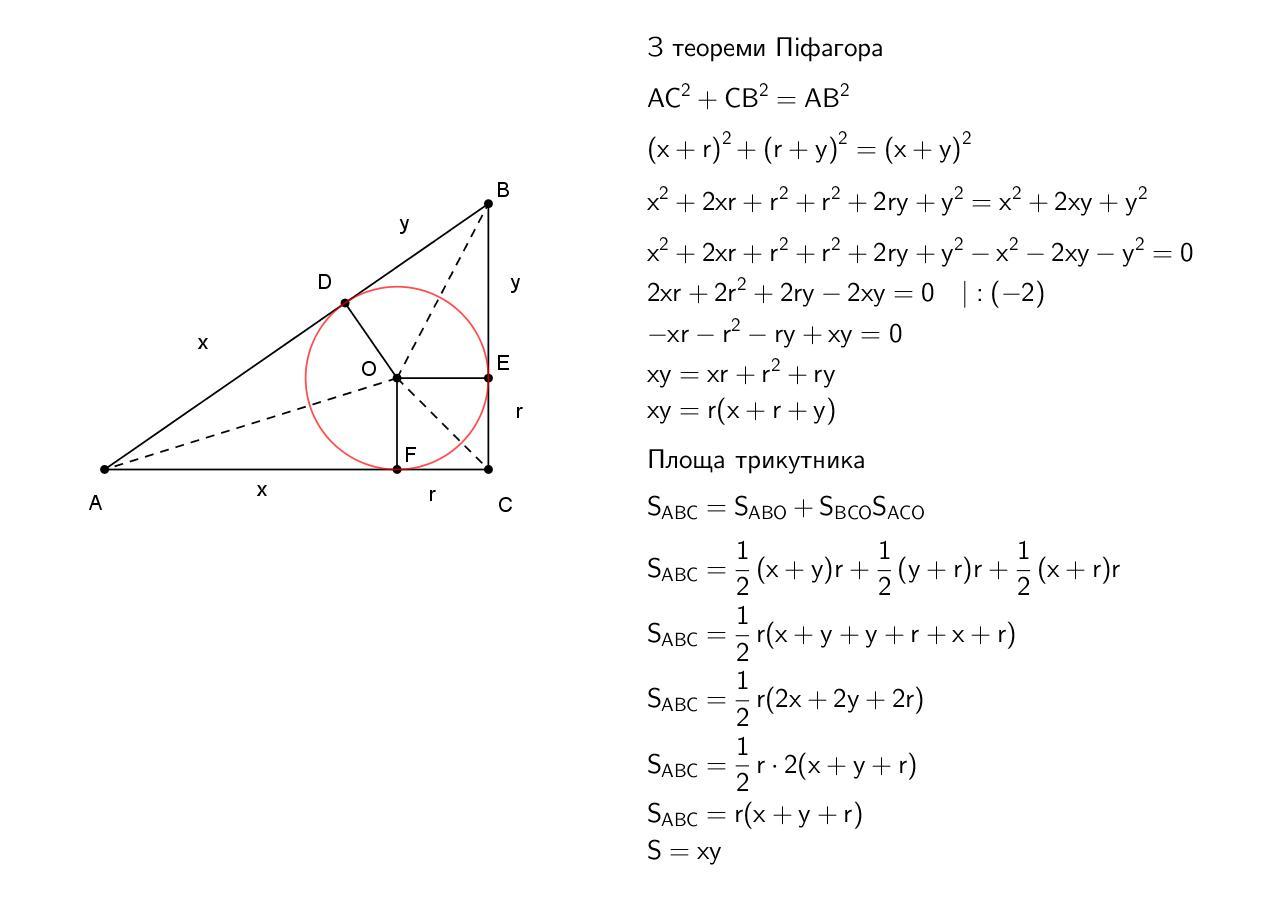
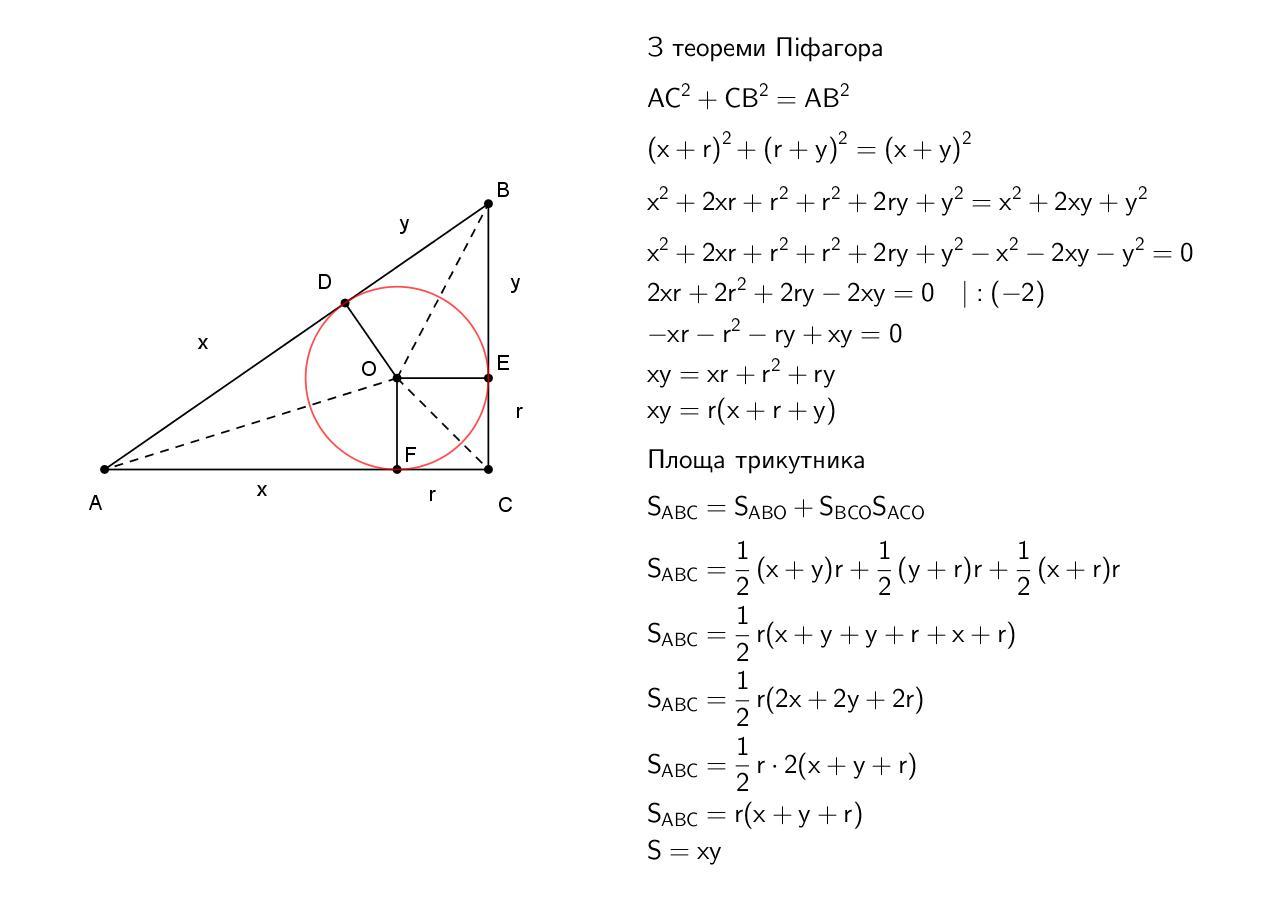
Доведіть, що коло, вписане у прямокутний трикутник, ділить його гіпотенузу на відрізки, добуток яких дорівнює площі цього трикутника.
Ответы 1
-
З теореми Піфагора
AC^2+CB^2=AB^2\\(x+r)^2+(r+y)^2=(x+y)^2\\x^2+2xr+r^2+r^2+2ry+y^2=x^2+2xy+y^2\\x^2+2xr+r^2+r^2+2ry+y^2-x^2-2xy-y^2=0\\2xr+2r^2+2ry-2xy=0\ \ \ |:(-2)\\-xr-r^2-ry+xy=0\\xy=xr+r^2+ry\\xy=r(x+r+y)
Площа трикутника
S_{ABC}=S_{ABO}+S_{BCO}+S_{ACO}\\S_{ABC}=\frac{1}{2}(x+y)r+\frac{1}{2}(y+r)r+\frac{1}{2}(x+r)r\\S_{ABC}=\frac{1}{2}r(x+y+y+r+x+r)\\S_{ABC}=\frac{1}{2}r(2x+2y+2r)\\S_{ABC}=\frac{1}{2}r\cdot2(x+y+r)\\S_{ABC}=r(x+y+r)\\S=xy
-
Автор:
koltenpfu9 - 2 года назад
-
5
-
-
Добавить свой ответ
Еще вопросы
-
Find and write six differences.
Bedroom
Bedroom
Living room
Kitchen
Alex's House
Bathroom
Laundry
*******
3 (bedroom)
4 (garage)
Bedroom
5 (living room)
Bedroom
Bathroom
Bathroom
Kitchen
Ben's House
1 (bathroom) Alex's house has got one
bathroom. Ben's house hasn't got one
bathroom. It has got two bathrooms.
2 (floors)
Bedroom
Living
room
Garage
-
Предмет:
Английский язык -
Автор:
joseph93 - 2 года назад
-
Ответов:
1 -
Смотреть
-
- алгебра 7 класс розвязок систем даю 100 баллов. распишите пожалуйста
-
Срочно!!!!!Стания, Зоя, Ян и Анух должны выполнить евклидово деление 77 на 8. Среди следующих ответов скажите, кто прав.Таня:77÷8=9,625Зоэ: 77 = 9 х 9-4Ян: 77 = 8 х 9 + 5Анух: 77 = 7 х 9 + 14
-
Предмет:
Математика -
Автор:
lisa65 - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Синтаксичний розбір речення: весна неповторна, красива, сумна
-
Предмет:
Українська мова -
Автор:
adolfo - 2 года назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
