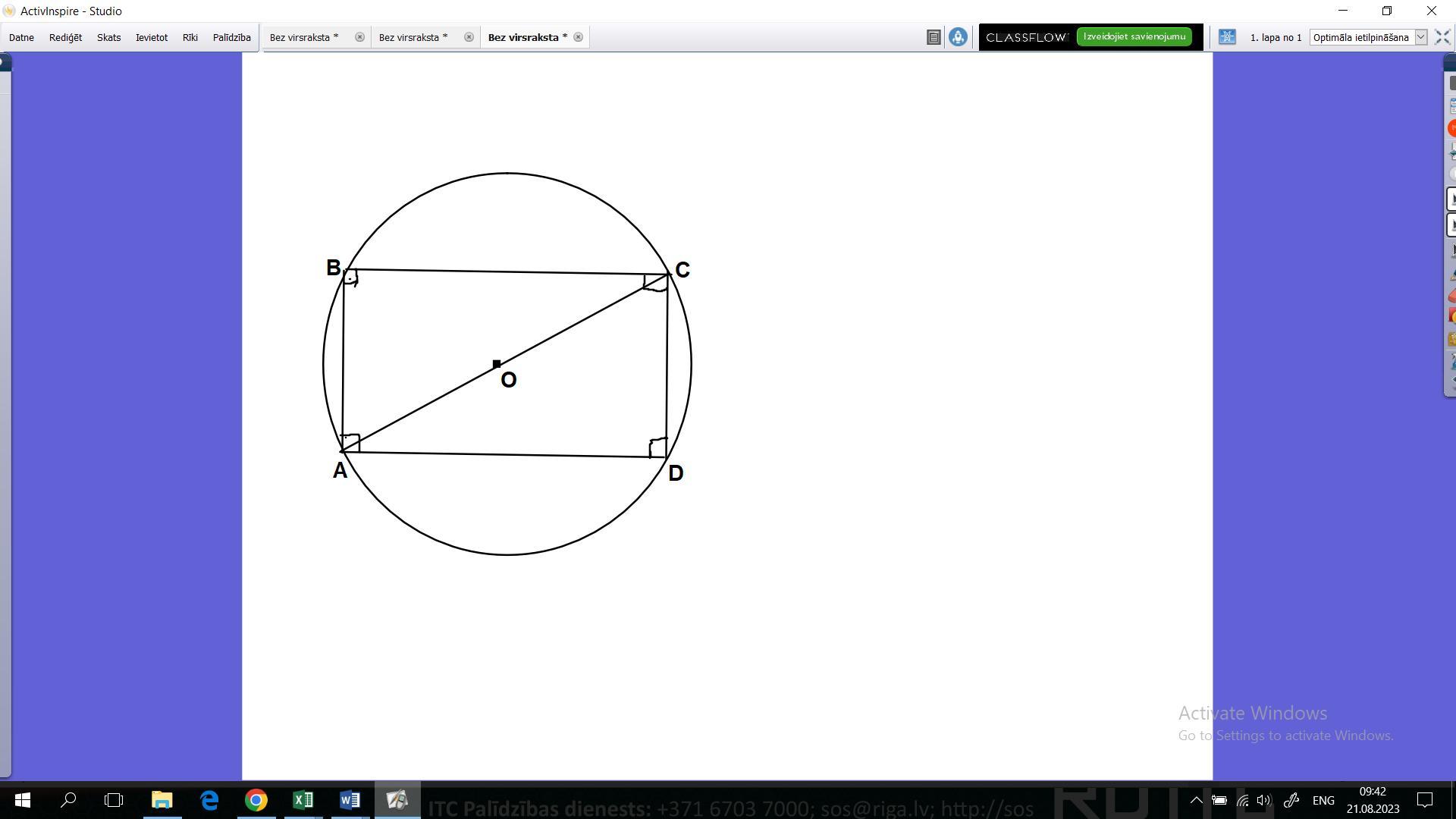
Дан параллелограмм, вершины которого лежат на одной окружности. Найди его меньшую сторону, если соотношение сторон этого параллелограмма 14:48, а радиус окружности — 100 см. Ответ: см.

Ответ: 5.6 cm

Объяснение:

Если вершины параллелограмма лежат на одной окружности, то этот параллелограмм вписан в окружность и такой параллелограмм является прямоугольником.

Причина сумма противоположных углов вписанного 4-х угольника равна 180°, но противоположный углы параллелограмма равны между собой =α=> α+α=180°=> α=90°. α -угол параллелограмма.

Центр описанной вокруг прямоугольника окружности находится на середине его диагонали. => AC= 100·2=200 cm

Обозначим АВ=14x , BC=48x

Тогда по теореме Пифагора имеем

AC²=AB²+BC² =>  200²=(14x)²+(48x)²

=> 400=196x²+2304x²

400=2500x²

25x²=4

x=2/5=0.4 cm

=> AB=0.4·14=5.6 cm