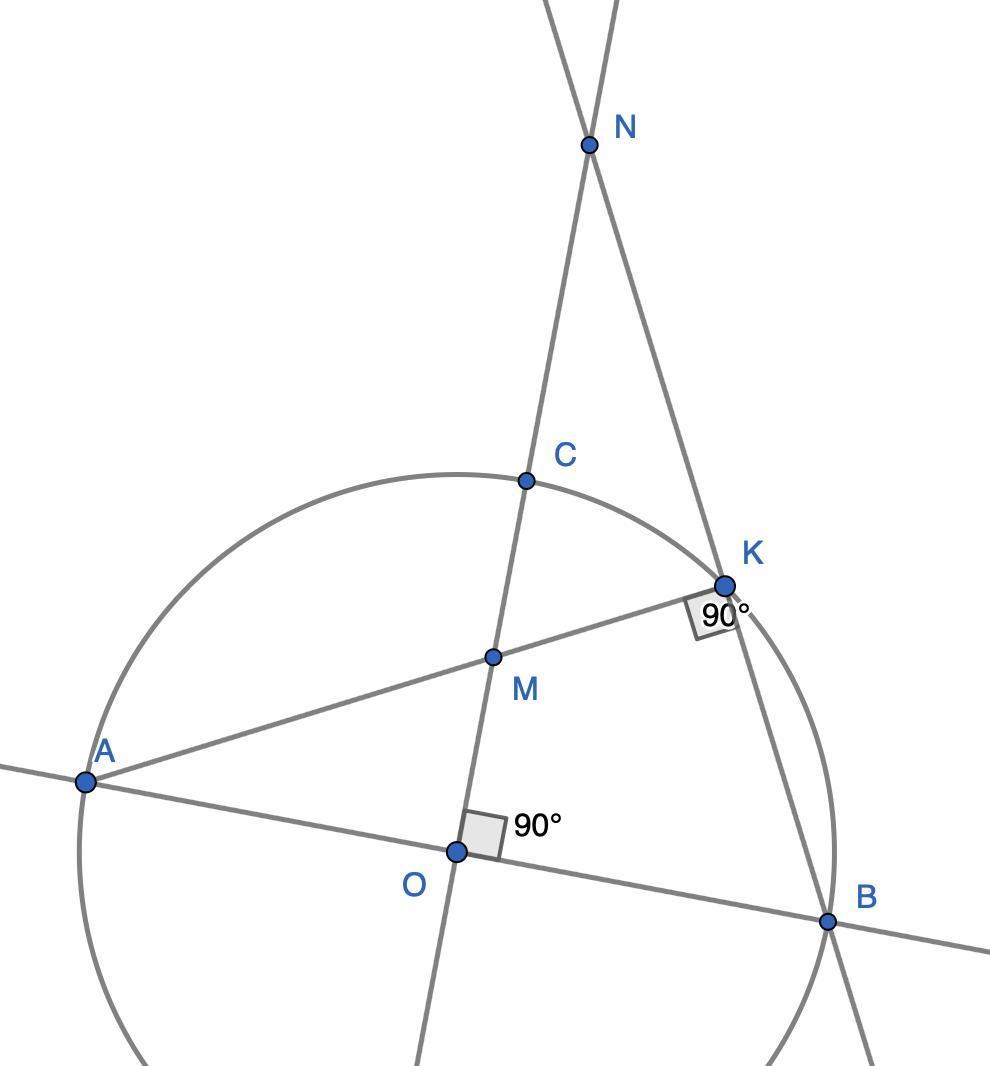
На колі з центром O і радіусом R, у якому проведено два взаємно перпендикулярних діаметри AB і CD, взято точку K. Хорда AK перетинає діаметр CD у точці M, а пряма BK – його продовження у точці N. Доведіть, що OM ∙ ON = R^2.

См. рисунокУгол AKB равен 90 градусов тк опирается на диаметр

Углы AOM и BON равны 90 градусов по условию

Треугольники ONB и AOM прямоугольные

2)

\angle ONB + \angle NBO = 90^\circ = \angle KAB + \angle ABK

так как NBO и ABK один и тот же угол мы получаем

\angle ONB = \angle KAB

Поэтому треугольники AOM и BON подобны (прямоугольные с одним и тем же острым углом)

3) из отношения сходственных сторон получаем

\displaystyle \frac{MO}{OB} = \frac{AO}{ON}\\\\OM\cdot ON = AO\cdot OB = R^2