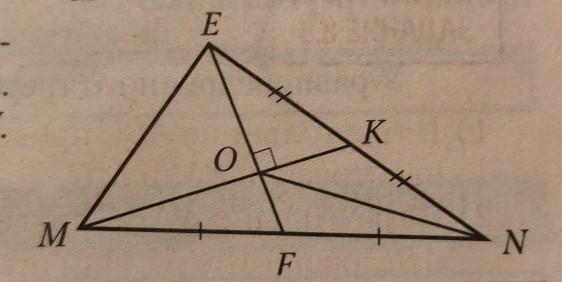
В треугольнике MEN, изображен- ном на рисунке, EF = 12, MK = 9. Найдите длины отрезков EM и ON.​

Рассмотрим треугольник MEN:

EF и MK - медианы, поскольку делят стороны напополам(см. рисунок).

По Т. про медианы в треугольнике имеем:

MO : OK = 2 : 1 = 2x : x, а также:

MK = MO + OK = x + 2x = 3x;

MK = 3x;

9 = 3x;

x = 3;

MO = 2x = 2 * 3 = 6(см).

OK = x = 3(см).

Полностью аналогично EO = 2x = 8см, а OF = x = 4см.

Дорисуем третью медиану NR(т. R лежит на ME).

NO / OR = 2x / x, так как т. O медиана NR делиться в данном соотношение(теорема выше).

Треугольник MOR подобен треугольнику NOK по второму признаку подобию треугольников.

Из подобия треугольников следует:

MO / OR = NO / OK;

6 / x = 2x / 3;

Решаем данную пропорцию крест-накрест:

18 = 2x^2;

x^2 = 9;

x = 3;

OR = x = 3(см).

ON = 2x = 6(см).

Угол EOK = углу EOM = 90°.

Треугольник EOM - прямоугольный.

В данном треугольнике по Т. Пифагора имеем:

ME^2 = MO^2 + EO^2 = 6^2 + 3^2 = 64 + 9 = 73;

ME = \sqrt{73}(см).

Ответ: ON = 6см, ME = \sqrt{73}см.