Дана трапеция ABCD с основаниями AD=13, BC=7. На плоскости выбрали точку E такую, что EA−→−+EB−→−=CD−→−. Найдите длину отрезка CE.

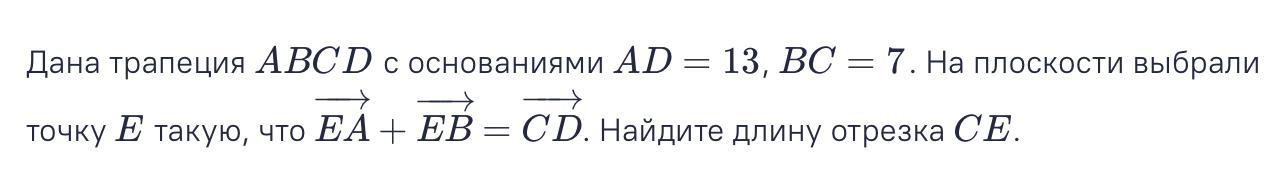
Ответ:

Для начала, построим трапецию ABCD с основаниями AD = 13 и BC = 7.

По условию задачи, точка E выбрана так, что вектор EA + EB равен вектору CD.Пусть точка E имеет координаты (x, y). Тогда вектор EA будет равен (x - Ax, y - Ay), где Ax и Ay - координаты точки A (0, 0).Вектор EB будет равен (x - Bx, y - By), где Bx и By - координаты точки B.Вектор CD будет равен (Dx - Cx, Dy - Cy), где Cx и Cy - координаты точки C, а Dx и Dy - координаты точки D.Из условия задачи, получаем следующую систему уравнений:x - Ax + x - Bx = Dx - Cxy - Ay + y - By = Dy - CyТак как точка A имеет координаты (0, 0), то Ax = Ay = 0.Также, точка B имеет координаты (7, 0), поэтому Bx = 7 и By = 0.Точка C имеет координаты (7, h), где h - высота трапеции.Точка D имеет координаты (0, h).Подставим значения в систему уравнений:x + x - 7 = Dx - Cxy + y = Dy - Cyx + x - 7 = Dx - Cx2y = Dy - CyТак как CD = AD - BC, то Dx - Cx = 13 - 7 = 6.Также, Dy - Cy = 0 - h = -h.Подставим эти значения в систему уравнений:x + x - 7 = 62y = -hУпростим уравнения:2x - 7 = 62y = -h2x = 13y = -h/2Решая первое уравнение, получаем x = 13/2 = 6.5.Таким образом, точка E имеет координаты (6.5, -h/2).Длина отрезка CE равна расстоянию между точками C и E.Расстояние между двумя точками на плоскости можно найти с помощью формулы:d = √((x2 - x1)² + (y2 - y1)²)В данном случае, координаты точки C равны (7, h), а координаты точки E равны (6.5, -h/2).Используя формулу, получаем:d = √((6.5 - 7)² + (-h/2 - h)²)= √((-0.5)² + (-3h/2)²)= √(0.25 + 9h²/4)= √(1/4 + 9h²/4)= √(9h² + 1)/2Таким образом, длина отрезка CE равна √(9h² + 1)/2.

Объяснение: