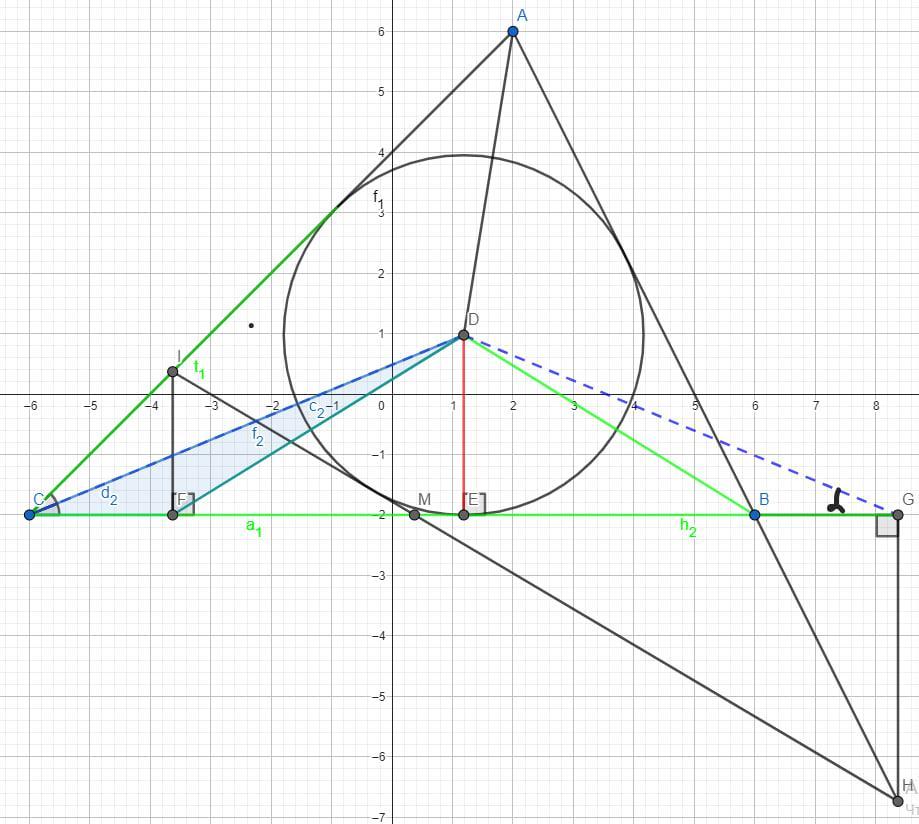
Дан остроугольный треугольник ABC. Взяли инцентр треугольника D (точка пересечения биссектрис треугольника) и опустили перпендикуляр на сторону BC. Пусть Точка пересечения перпендикуляра и стороны будет называться E. На луче EC отложили отрезок EF который равен EB. Получили отрезок CF. С точки F подняли перпендикуляр к прямой BC до пересечения со стороной AC. Назовём точку пересечения перпендикуляра и стороны точкой I. На луче EB отложили отрезок EG равен EC. С точки G подняли перпендикуляр к прямой BC до пересечением с продолжением стороны AB. Получили точку H. Доказать, что прямая IH - касательная к окружности с центром в точке D и радиусом DE

Ответ:

Давайте рассмотрим данную конструкцию более подробно и докажем, что прямая IH действительно является касательной к окружности с центром в точке D и радиусом DE.

1. Обозначим угол A треугольника ABC как α.

2. Так как D - инцентр треугольника ABC, то угол BDC равен половине угла B, то есть угол BDC равен α/2.

3. Поскольку D - инцентр, BD и CD - биссектрисы углов B и C соответственно. Таким образом, угол BDI и угол CDI также равны α/2.

4. Теперь обратим внимание на треугольник BDE. Мы знаем, что угол BDE равен углу BDI, так как они оба равны α/2. Поэтому BDE - прямоугольный треугольник.

5. Рассмотрим треугольник BEF. Мы знаем, что отрезок EF равен EB, что делает треугольник BEF равнобедренным, и угол EFB равен α/2.

6. Теперь рассмотрим треугольник FCI. У нас есть угол FCI, равный α/2, и угол CFI, который равен 90 градусов, так как CF - перпендикуляр к BC.

7. Из углового уравнения для треугольника FCI следует, что угол FIC равен 90 - α/2.

8. Рассмотрим треугольник DEI. У нас есть угол DIE, равный 90 градусов, так как DE - радиус окружности, и угол EDI, который равен углу BDI, то есть α/2.

9. Таким образом, угол DIE + угол FIC = (90° + α/2) + (90° - α/2) = 180°.

10. Это означает, что прямая IH пересекает DE под углом 90 градусов, что делает ее касательной к окружности с центром в точке D и радиусом DE.

Таким образом, прямая IH действительно является касательной к данной окружности.