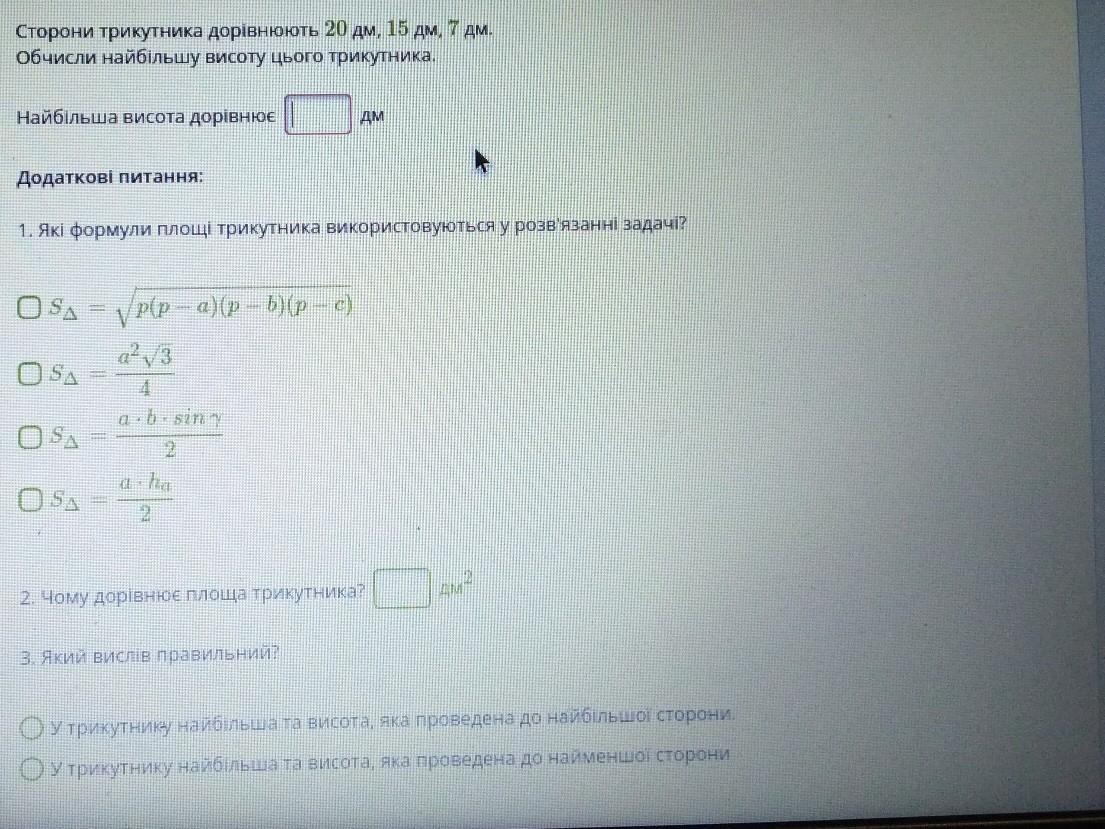
Сторони трикутника дорівнюють 20 ДМ. 15 Дм, дм. 7 Обчисли найбільшу висоту цього трикутника. Найбільша висота дорівнює Додаткові питання: 1. Які формули площі трикутника використовуються у розв'язаннi задачі? OS= p(p-a)(p-b)(p-c) OSA OSA OSA = a23 4 a.b-siny 2 ДМ a ha​

Для знаходження найбільшої висоти трикутника можна використовувати формулу площі трикутника:

S = 1/2 * a * ha

де:

S - площа трикутника,

a - одна зі сторін трикутника,

ha - висота, яку ми шукаємо.

Також, для трикутника, можна використати формулу Герона для обчислення площі, де p - полупериметр трикутника:

S = √(p(p - a)(p - b)(p - c))

Знаючи площу S та одну зі сторін a, можна обчислити висоту ha. Завдання полягає в обчисленні найбільшої можливої висоти, тому для цього нам потрібно знайти максимальну площу для заданих сторін трикутника.

З формули Герона відомо, що площа трикутника максимальна, коли всі сторони рівні. Отже, найбільша висота буде в трикутнику із сторонами 20 ДМ, 20 ДМ і 20 ДМ.

Тепер можемо обчислити висоту:

p = (20 + 20 + 20) / 2 = 30 ДМ (полупериметр)

S = √(30(30 - 20)(30 - 20)(30 - 20)) = √(30 * 10 * 10 * 10) = √(30000) = 100√3 ДМ²

Отже, найбільша висота (ha) дорівнює S / a = (100√3) / 20 = 5√3 ДМ.

Найбільша висота трикутника дорівнює 5√3 ДМ.