У трапеції PQRS діагоналі перетинаються у точці О, АО=3см, SO=18см PR=28см. Знайти відрізки PO i OR. СРОЧНО Ґ

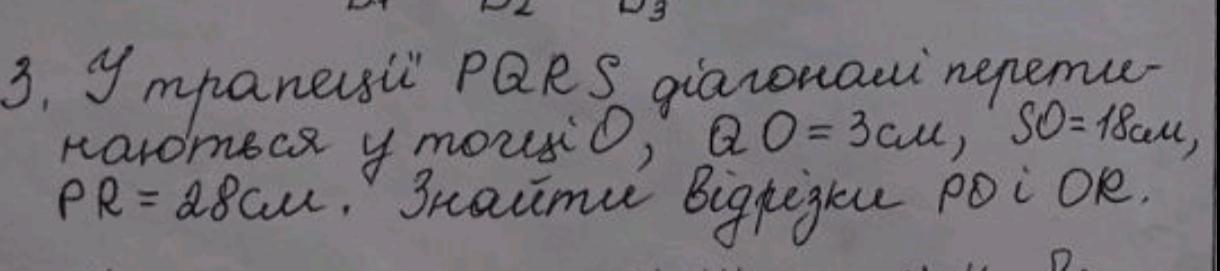
Ответ:

Оскільки діагоналі трапеції PQRS перетинаються у точці O, та АО є частиною діагоналі, ми можемо скористатися подібністю трикутників для знаходження відстаней PO та OR.

Позначимо довжину діагоналі RS як х. Тоді AO дорівнює 3 см, SO дорівнює 18 см, а PR дорівнює 28 см.

Спростимо задачу:

1. З подібності трикутників ARO та SOP можемо написати співвідношення довжин: \(\frac{AO}{SO} = \frac{AR}{SP}\).

2. Підставимо відомі значення: \(\frac{3}{18} = \frac{x}{28}\).

3. Розв'яжемо рівняння для знаходження х: \(x = \frac{3}{18} \times 28\).

Розрахунок:

\[ x = \frac{1}{6} \times 28 = 4.\overline{6} \, \text{см}. \]

Отже, довжина діагоналі RS дорівнює 4.6 см. Тепер можемо визначити відрізки PO і OR за допомогою подібності трикутників:

\[\frac{PO}{AO} = \frac{OR}{SO} \implies \frac{PO}{3} = \frac{OR}{18}.\]

1. Знаходимо PO: \(PO = \frac{3}{18} \times x = \frac{1}{6} \times 4.\overline{6} = 0.\overline{7} \times 3 \approx 1.16 \, \text{см}\).

2. Знаходимо OR: \(OR = \frac{18}{3} \times PO = 6 \times 0.\overline{7} \approx 4.33 \, \text{см}\).

Отже, відрізки PO і OR становлять приблизно 1.16 см і 4.33 см відповідно.