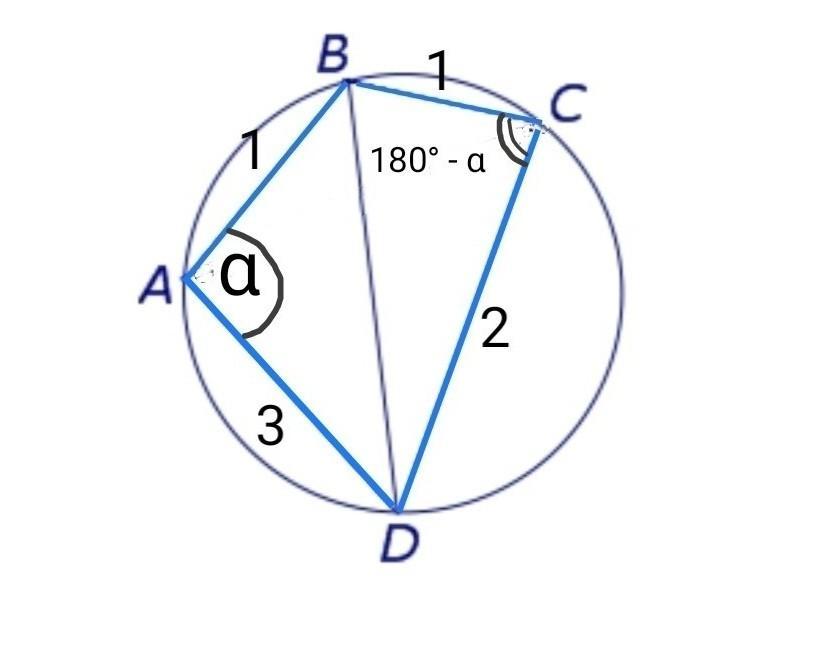
Четырехугольник ABCD вписан в окружность, AB = BC = 1, CD = 2, AD = 3. Найдите диагональ BD

Ответ:

√7.

Объяснение:

1 По теореме косинусов в ∆ DAB

DB² = DA² + AB² - 2•DA•AB•cosA =

= 3² + 1² - 2 • 3 • 1 • cosα = 10 - 6cisα.

2. По свойству вписанного четырёхугольника

∠ А + ∠ С = 180°.

Так как ∠ А = α, то ∠ С = 180° - α.

3. По теореме косинусов в ∆ DСB

DB² = DС² + СB² - 2•DС•СB•cosС =

= 2² + 1² - 2 • 2 • 1 • cos(180° - α) = 5 - 4(- cosα) = 5 + 4cosα.

4. Составим и решим уравнение:

10 - 6cisα = 5 + 4cosα

10 - 5 = 4cosα + 6cosα

5 = 10•cosα

cosα = 5/10

cosα = 1/2.

5. Подставим полученное значение в равенство:

DB² = 5 + 4cosα = 5 + 4•1/2 = 7, тогда

DB = √7.