Параллельные стороны трапеции равны 60 см и 20 см, а боковые стороны - 13 см и 37 см. Найдите площадь трапеции.​

Ответ:

**********

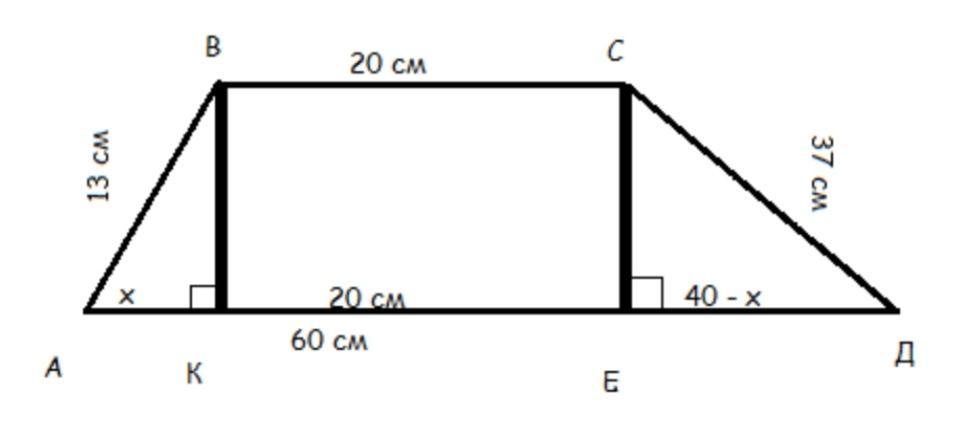
Дано : АВСD - трапеция

АВ= 13 см, СД= 37 см.

ВС= 20 см, АД = 60 см

Найти: S трапеции

решение:

Пусть , АК = х см, КЕ= ВС= 20 см, тогда ЕД = АД - АК - КЕ = 60 - 20 - х = (40 - х) см. Теперь по теореме Пифагора имеем :

ВК ^2 = 13^2 - х^2

СЕ^2 = 37^2 - (40-х)^2

13^2-х^2=37^2 - (40- х)^2

169 - х^2=1369-1600+80х- х^2

-х^2+х^2= -231 - 169+ 80х

-80х=-400

х=5

Значит АК= 5 см, тогда ВК^2=13^2 -5^2

ВК^2 =169-25

ВК=√ 144

ВК = 12(см)

S тр. = ВС+АД/ 2 * 12= 480 (см ^2)

Ответ: S АВСД = 480 см²

************

Объяснение: