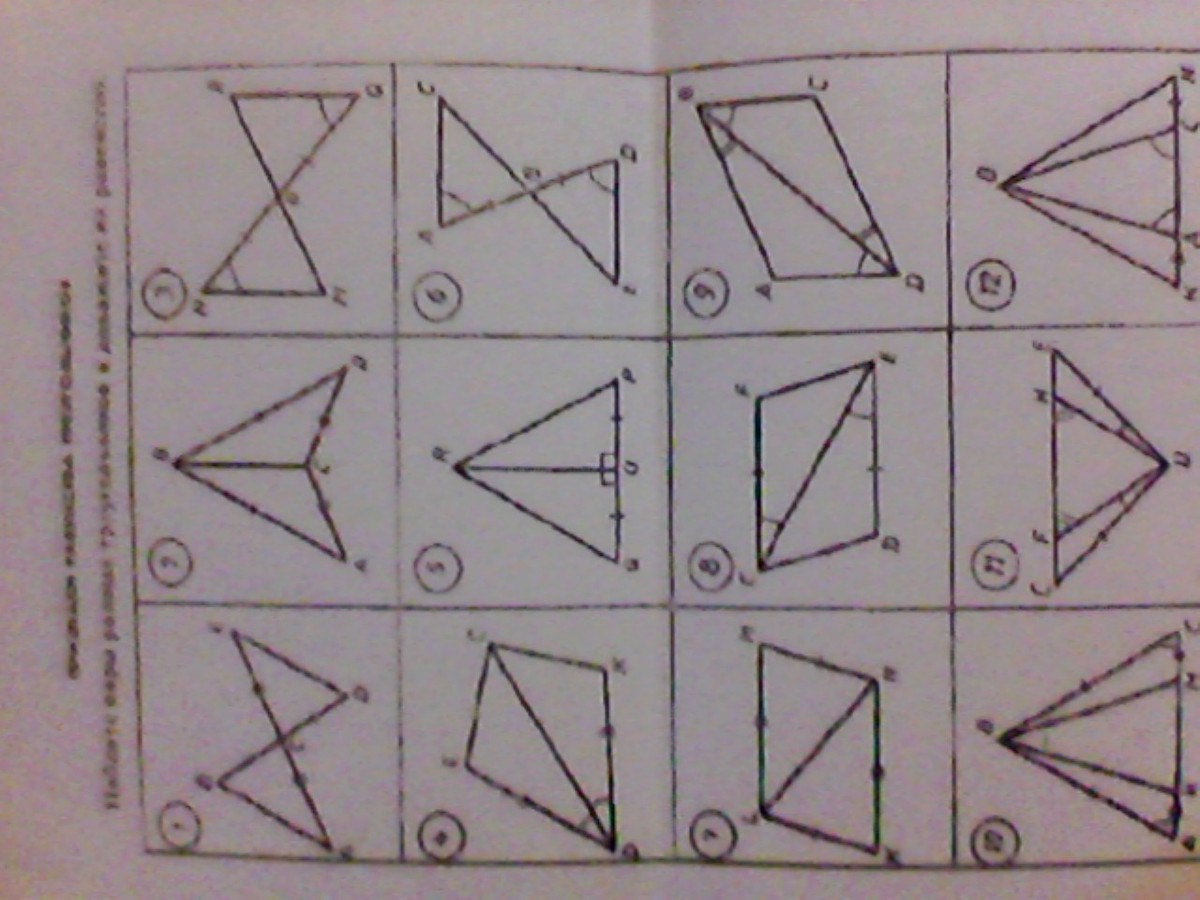
Найдите пары  равных треугольников  и докажите их равенство. Помогите  пожалуйста очень надо. Помогите пожалуйста, завтра сдавать уже:(

1. АС = СЕ, BC = CD по условию,   ∠ACB = ∠DCE как вертикальные, ⇒   ΔАСВ = ΔDCE по двум сторонам и углу между ними.2. АВ = BD, AC = CD по условию,    ВС - общая сторона для треугольников АВС и DBC, ⇒   ΔАВС = ΔDBC по трем сторонам.3. MP = PQ, ∠MNP = ∠RQP по условию,     ∠MPN = ∠RPQ как вертикальные, ⇒   ΔMNP = ΔRQP по стороне и двум прилежащим к ней углам.4. DE = DK, ∠ЕDC = ∠KDC по условию,    DC - общая сторона для треугольников ЕDC и KDC, ⇒     ΔЕDC = ΔKDC по двум сторонам и углу между ними.5. QO = OP по условию, ∠ROQ = ∠ROP = 90°,   RO - общая сторона для треугольников ROQ и ROP, ⇒   ΔROQ = ΔROP по двум сторонам и углу между ними.6. AB = BD, ∠BAC = ∠BDE по условию,   ∠ABC  = ∠DBE как вертикальные, ⇒   ΔABC  = ΔDBE по стороне и двум прилежащим к ней углам.7. LK = NM, LM = NK по условию,   LN - общая сторона для треугольников LKN и NML, ⇒   ΔLKN = ΔNML по трем сторонам.8. FC = DE, ∠FCE = ∠DEC по условию,   СЕ - общая сторона для треугольников FCE и DEC, ⇒   ΔFCE = ΔDEC по двум сторонам и углу между ними.9. ∠ADB = ∠CBD, ∠ABD = ∠CDB по условию,   BD - общая сторона для треугольников ADB  и CBD, ⇒   ΔADB = ΔCBD по стороне и двум прилежащим к ней углам.10. ВР = ВС, РК = СМ по условию,   ∠ВРК = ∠ВСМ так как треугольник РВС равнобедренный, ⇒   ΔВРК = ΔВСМ по двум сторонам и углу между ними.Из равенства треугольников следует, что ВК = ВМ,ВР = ВС по условию,РМ = РК + КМ, СК = СМ + КМ, а так как РК = СМ, тоРМ = СК, ⇒ ΔРВМ = ΔСВК по трем сторонам.11. DC = DE, ∠CDF = ∠EDH - по условию,   ∠DCF = ∠DEH как углы при основании равнобедренного треугольника CDE, ⇒   ΔCDF = ΔEDH по стороне и двум прилежащим к ней углам.Из равенства треугольников следует, что DF = DH и  CF = EH, но тогда и CH = EF, ⇒ ΔCDH = ΔEDF по трем сторонам.12. ВА = ВС так как ∠ВАС = ∠ВСА и, значит ΔАВС равнобедренный,       АК = СN по условию,

     ∠ВАК = ∠ВСN как углы, смежные с равными углами, ⇒      ΔВАК = ΔВСN по двум сторонам и углу между ними. Из равенства треугольников следует, что BK = BN, КС = КА + АС, NA = NC + AC, а так как КА = NC, то КС = NA ВА = ВС по условию, ⇒ ΔКВС = ΔNBA по трем сторонам.