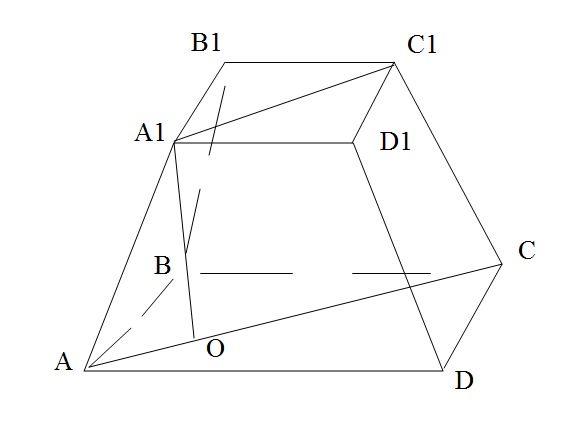
В правильный четырехугольной усеченной пирамиде площадь диагонального сечения равна 7√2 см^2 . Стороны оснований равны 5 см и 2 см . Найдите объем усеченной пирамиды.

Дана правильная четырехугольная усеченная пирамида ABCDA1B1C1D1. ABCD и A1B1C1D1 - квадраты, со сторонами 5 и 2 см соответственно.Площадь диагонального сечения - это площадь АА1С1С (трапеции, А1О-высота).S (AA1C1C) = \frac{A1C1+AC}{2} *A1OA1C1 = \sqrt{ 2^{2}+ 2^{2} } =2 \sqrt{2} AC= \sqrt{ 5^{2} + 5^{2} } =5 \sqrt{2} 7 \sqrt{2} = \frac{7 \sqrt{2} }{2} * A1OA1O = 2Объем усеченной пирамиды: V= \frac{1}{3}*h*(S1+S2+ \sqrt{S1S2} )S1 = 5*5=25S2 = 2*2=4V= \frac{1}{3} *2*(29+10)=26