-
30 баллов за решение!
Применение теоремы о трех перпендикулярах Из точки M к плоскости ромба ABCD проведен перпендикуляр BM. Известно, что AB=6 cm,угол BAD = 60 градусов,а расстояние от точки M до прямой CD равно 6 см. Выполните дополнительное построение и найдитерасстояние от точки M до диагонали AC.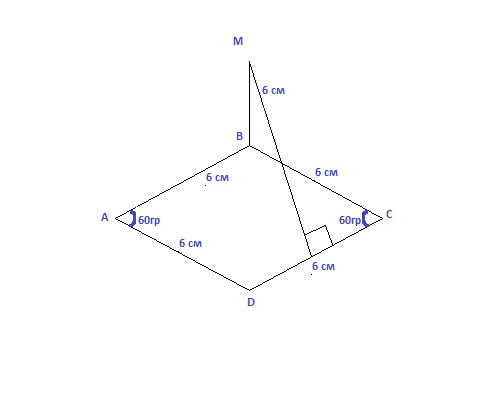
Ответы 1
-
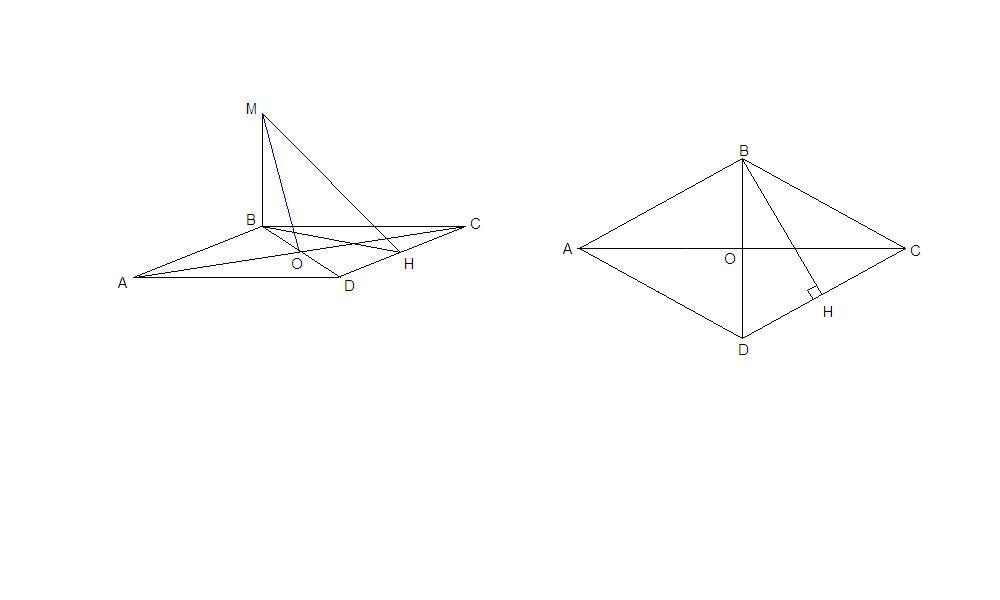
Если в ромбе угол равен 60°, то его меньшая диагональ равна стороне (АВ = AD как стороны ромба, ΔАBD равнобедренный с углом 60°, значит и остальные углы по 60°, т.е. ΔАВD равносторонний).Расстояние от точки до прямой - длина перпендикуляра, проведенного из точки к прямой.Пусть Н - середина CD, тогда BH - медиана и высота в равностороннем треугольнике BCD. ВН⊥CD.ВН - проекция МН на плоскость АВС, значит МН⊥CD по теореме о трех перпендикулярах.МН = 6 см - расстояние от точки М до прямой CD.ВН = ВС√3/2 = 6√3/2 = 3√3 см как высота равностороннего треугольникаИз ΔМВН по теореме Пифагора:МВ = √(МН² - ВН²) = √(36 - 27) = √9 = 3 смВО⊥АС так как диагонали ромба перпендикулярны.ВО - проекция МО на плоскость АВС, значитМО⊥АС по теореме о трех перпендикулярах.МО - искомое расстояние от точки М до прямой АС.ВО = BD/2 = 6/2 = 3 смИз ΔМВО по теореме Пифагора:МО = √(МВ² + ВО²) = √(9 + 9) = √18 = 3√2 см
-
Автор:
cuddles10nx - 2 года назад
-
4
-
-
Добавить свой ответ
Еще вопросы
-
Перечислите
эры и периоды, на которые делится время развития земной коры. Отложения каких
периодов обнаружены на территории Ростовской области. Какие из них выходят на дневную поверхность, а какие
скрыты буровыми скважинами.-
Предмет:
Другие предметы -
Автор:
sherman - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Даны два квадрата, диагонали которых равны 12 и 13. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.
-
Предмет:
Алгебра -
Автор:
pirateawwk - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Помогите!!!Что к чему относится.Профессии:Шахтер,учитель,художник,хлебороб,домашняя хозяйка,дворник,программист,менеджер,космонавт,продавец,полицейский.Характеристики труда:Постоянный,временный,простой,сложный,умственный,физический,оплачиваемый,безвозмездный.добровольный,принудительный,ручной,автоматизированный,творческий,традиционный,коллективный,индивидуальный.
-
Предмет:
Обществознание -
Автор:
maggie-moo - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
в костяном горшочке,сладенькая каша,варилась на солнце-составить загадку
-
Предмет:
Русский язык -
Автор:
rufioge7z - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
