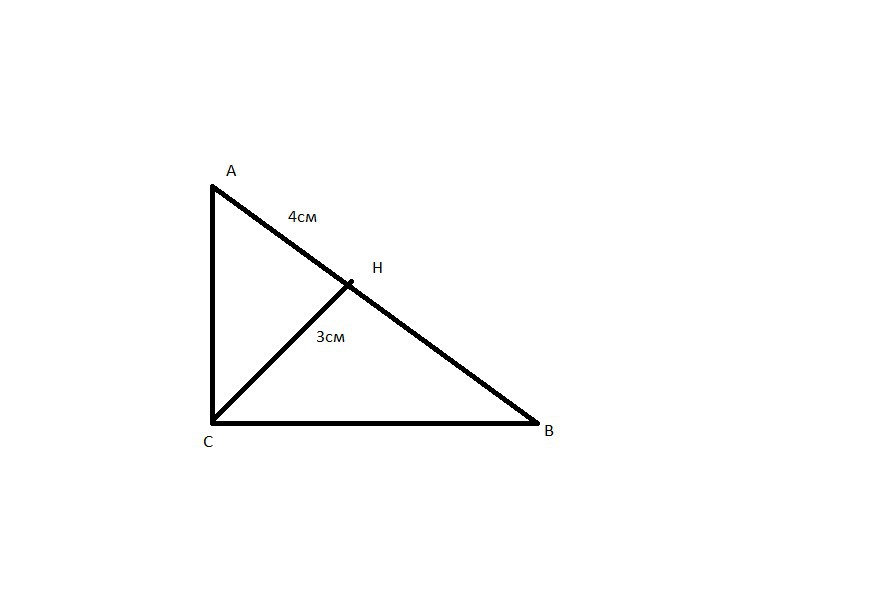
В треугольнике АВС угол С равен 90 градусов, СН - высота, АН=4, СН=3. Найдите ВС.

Рассмотрим треугольник АСН - он также прямоугольный (свойство высоты)Нам в нем известны два катета СН и АН, по т.Пифагора мы можем найти гипотенузу АС.AC= \sqrt{ AH^{2} + CH^{2} } AC= \sqrt{ 4^{2} + 3^{2} } AC= \sqrt{ 16 + 9 } AC= \sqrt{ 25} AC=5cmРассмотрим треугольник АВС:Воспользуемся 2 формулами для нахождения площади:S= \frac{h*c}{2} h- высота, с - в нашем случае гипотенуза (сторона, к которой проведена высота)S= \frac{a*b}{2} a,b - катеты \frac{a*b}{2} = \frac{h*c}{2} a*b=c*hнам известна высота(3см) и  катет АС - пусть "а" (5см)5b=3cвыразим cc= \frac{5b}{3} Далее с помощью теоремы Пифагора найдем катет BС (b) c^{2} = a^{2} +b^{2} Заменим "c" на наше выражение ( \frac{5b}{3} )^{2} = 5^{2} +b^{2} \frac{25 b^{2} }{9}=25+ b^{2} 25b^{2}= 225+9b^{2} 25b^{2}-9b^{2}=225 16b^{2}=225 b= \sqrt{ \frac{225}{16} } b= \frac{15}{4} b=3,75 cm