Задать вопрос Регистрация
Помочь другим

  • Только с решением, пожалуйста.

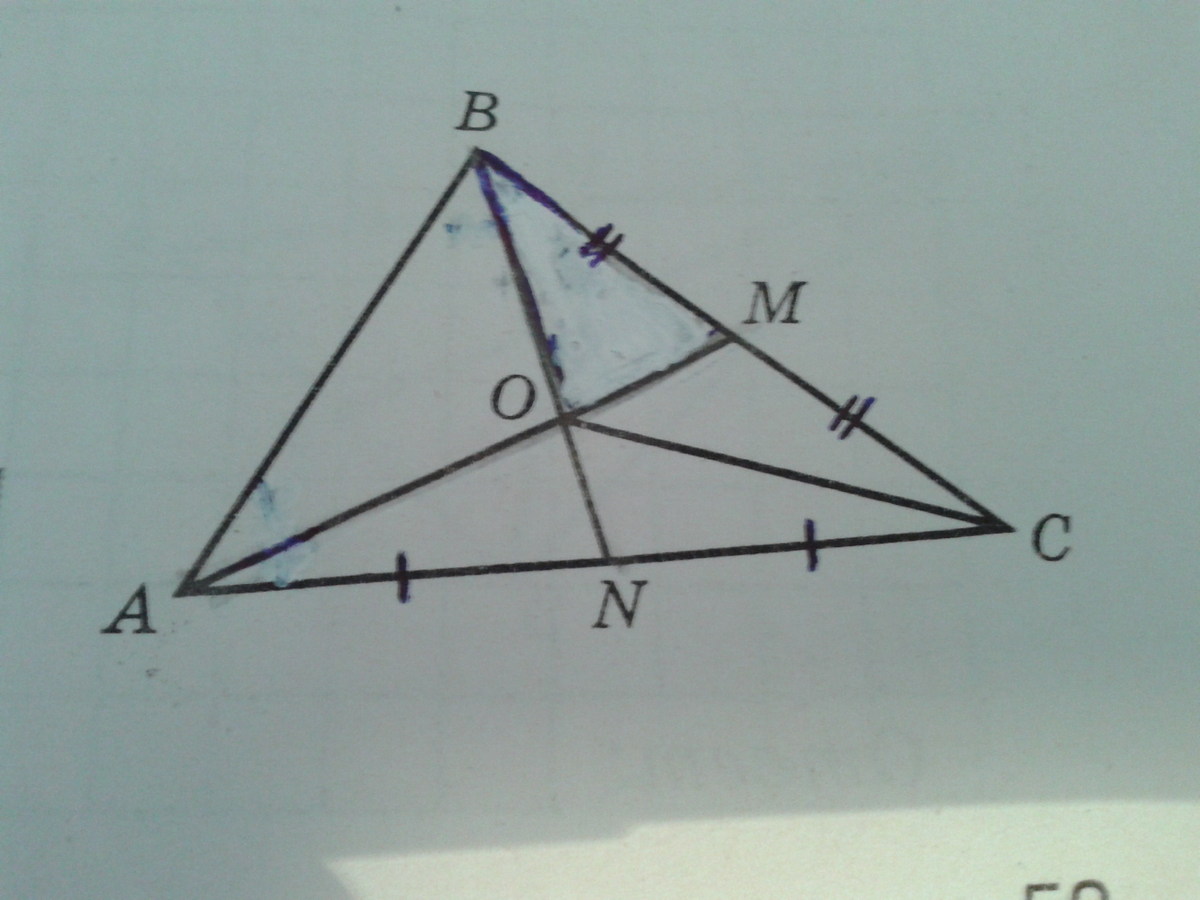
    На рисунке AM и BN - медианы треугольника ABC. Укажите треугольник, площадь которого равна площади треугольника BOM.

    question img

Ответы 1

  • углы AON=BOM вертикальные Медианы треугольника пересекаются и точкой пересечения делятся в отношении 2:1 считая от вершины ВО=\frac{2}{3}BN,  ОN=\frac{1}{3}BN, AО=\frac{2}{3}AM,  OM=\frac{1}{3}AM, S_{BOM}=\frac{1}{2}*BO*OM*sin(BOM)=\frac{1}{2}*\frac{2}{3}BN*\frac{1}{3}AM*sin(BOM)= \\ =\frac{1}{9}BN*AM*sin(BOM) \\ \\ S_{AON}=\frac{1}{2}*AO*ON*sin(AON)=\frac{1}{2}*\frac{2}{3}AM*\frac{1}{3}BN*sin(AON)= \\ =\frac{1}{9}BN*AM*sin(AON) \\ \\ S_{BOM}=S_{AON}Площадь треугольника AON равна площади треугольника ВОМ

    • Автор:

      dixon
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years