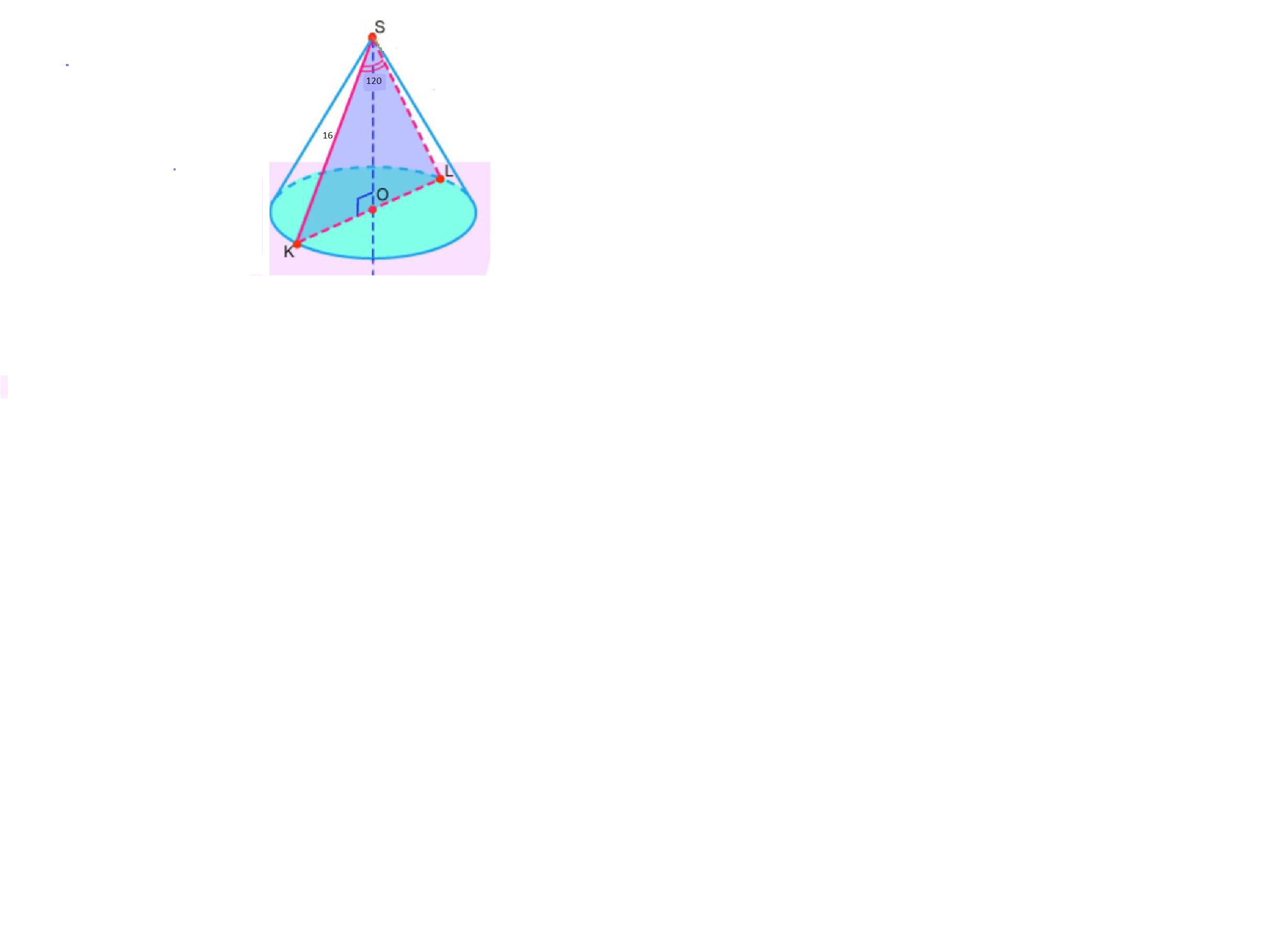
Образующая конуса равна 16 см. Угол при вершине его осевого сечения 120 градусов. Вычислите объем конуса. помогите пожалуйста! и решение если можно максимально подробно расспишите

SO -  высота конусаSK=SL  - образующие конусаOK=OL - радиусыΔ KSL  - осевое сечение конуса\ \textless \ KSL -  угол при вершине осевого сечения конусаV= \frac{1}{3} \pi R^2*H\ \textless \ KSL=120^\circ SL=16  смV= \frac{1}{3} \pi *OL^2*SOРассмотрим осевое сечение конуса:Δ KSL -  равнобедренный треугольник, так как SK=SL=16  смSO -  высота, медиана и биссектриса Δ KSL, т. е. SO ⊥ KLOL=OK   и \ \textless \ KSO=\ \textless \ LSO=60^\circ Δ SOL - прямоугольный  (\ \textless \ SOL=90^\circ )\ \textless \ LSO=60^\circ ,  значит  \ \textless \ SLO=30^\circ Катет прямоугольного треугольника, лежащий против угла в 30 градусов, равен половине гипотенузы.Значит SO= \frac{1}{2}SL SO= \frac{1}{2}*16=8  смПо теореме Пифагора найдем OL= \sqrt{SL^2-SO^2} = \sqrt{16^2-8^2} = \sqrt{(16-8)(16+8)} = \sqrt{8*24}= \sqrt{8*8*3}=8 \sqrt{3}  смV= \frac{1}{3}* \pi *(8 \sqrt{3})^2*8= \frac{1}{3}* \pi *64*3*8=512 \pi  см³Ответ: 512 \pi  см³