-
Написать уравнение окружности.
см.фото
Решение:
Уравнение окружности имеет вид (х - а)2 + (у - b)2 = R2
Чтобы написать уравнение окружности надо знать
координаты центра О(a; b) и
радиус окружности R = OA
Найдем координаты точки А по формулам:
[tex] x_{k} = \frac{x_{A} + x_{B}}{2} ; y_{k} = \frac{y_{A} + y_{B}}{2} [/tex]
Тогда ... = [tex]( x_{A} + ...) /2
[/tex]
[tex] x_{A} = ...[/tex]
Аналогично ... = [tex] (y_{A} + ...)/2[/tex]
[tex] y_{A} [/tex] = ...
Значит точка А имеет координаты А (... ; ...)
По формулам [tex] x_{O} = \frac{ x_{A} + x_{C} }{2} [/tex] ; [tex] y_{O} = \frac{ y_{A} + y_{C} }{2} [/tex]
найдем координаты точки О ( ... ; ...)
Найдем длину отрезка ОА по формуле:
OA = [tex] \sqrt{ (x_{O} - x_{A})^{2} + (y_{O} - y_{A})^{2} } [/tex]
OA = ...
Тогда уравнение окружности
(x - ...)[tex] ^{2} [/tex] + (y - ...)[tex]^{2} [/tex] = ...
Там где "..." - нужно вставить пропущенное.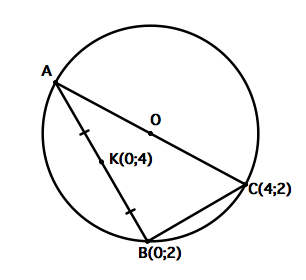
Ответы 1
-
Введем систему координат. Нарисуй как обычно взаимно перпендикулярные оси и Расположи точки. (0;2) (2;4) и ( 0; 4)Точка А находится на таком же расстоянии от К, как и В.Понятно что ВК = 2, значит АК тоже равно 2. Поэтому координата Точки А (0;6)Рассмотри треугольник АВС. На нашей картинке хорошо видно, что он прямоугольный. Найдем гипотенузу по теореме Пифагора 4²+4²= 32Ав= 4√2, АО=ОС= 2√2Точка О - центр окружности имеет координаты. (2; 4) видно на картинке.Ответ (х-2)²+(у-4)²= (2√2)²
-
Автор:
emelineazyo - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
(-3a^3b)(-2ab^2)(-5a^3b^7)=??? решите подробно пожалуйста
-
Предмет:
Алгебра -
Автор:
ameliab1e9 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
За два куска материи заплатили 560 рублей. В одном куске было 27 метров материи, а в другом 43 метра такой же материи. Сколько стоит каждый кусок материи?
-
Предмет:
Математика -
Автор:
aubrie - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
почему Александр Македонский жестоко расправился с жителями Тира?
-
К 240 г воды добавили 60 г соли.Сколько процентов соли содержится в растворе?
-
Предмет:
Алгебра -
Автор:
masonbrennan - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
