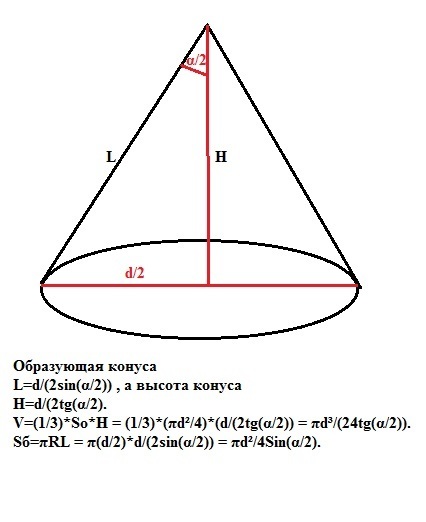
Найдите объем и боковую поверхность конуса, диаметр основания которого равен d, а угол при вершине осевого сечения равен альфа

Осевое сечение конуса - равнобедренный треугольник с углом при вершине, равным "α". Высота конуса - высота этого треугольника, является и медианой и биссектрисой. Следовательно, образующая конуса (гипотенуза прямоугольного треугольника с катетами, равными высоте конуса и радиусу основания) L=d/(2sin(α/2)) , а высота конусаН=d/(2tg(α/2).Тогда объем конуса равенV=(1/3)*So*H = (1/3)*(πd²/4)*(d/(2tg(α/2)) = πd³/(24tg(α/2)).Sб=πRL = π(d/2)*d/(2sin(α/2)) = πd²/4Sin(α/2).