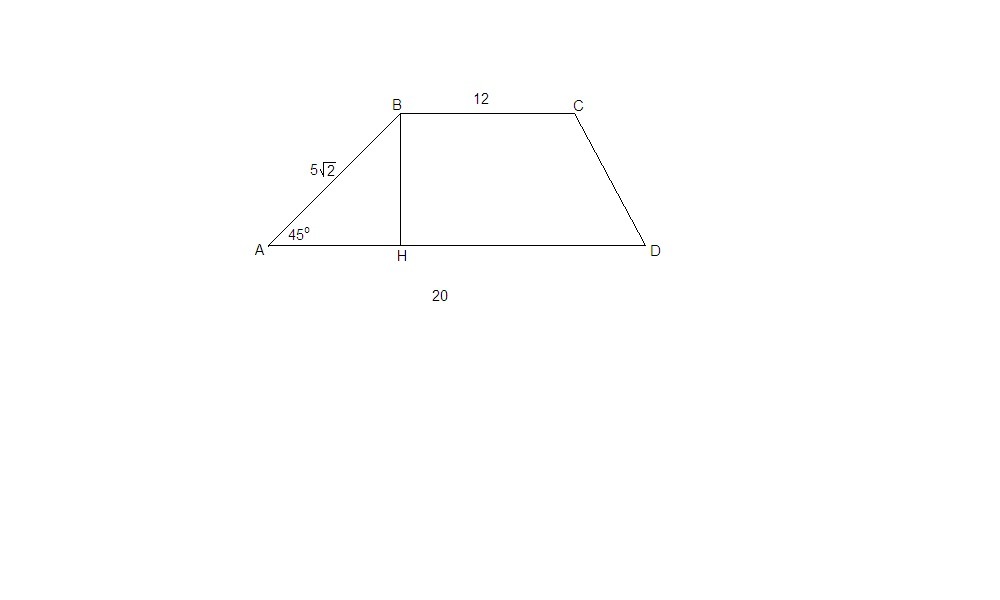
Боковая сторона трапеции ABCD (AB|| CD), равная 5√2 см, образует с большим основанием угол в 45 º . Основания равны 12см и 20см.

а) Вычислите площадь трапеции. б) Докажите, что треугольники ABD и BAС имеют равные площади.

а) Проведем высоту ВН.Sabcd = (AD + BC)/2 · BHΔАВН: ∠АНВ = 90°, ∠ВАН = 45°, ⇒ ∠АВН = 45°, ⇒             треугольник равнобедренный.Пусть АН = ВН = x, по теореме Пифагора:x² + x² = AB²2x² = 50x² = 25x = 5            (x = - 5 не подходит по смыслу задачи)ВН = 5 смSabcd = (20 + 12)/2 · 5 = 16 · 5 = 80 см²б) В условии задачи ошибка: вероятно, надо доказать равенство площадей ΔABD и ΔDAС.Площади этих треугольников равны, так как они имеют общее основание AD и одинаковую высоту, равную 5 см.