-
1.Найдите <CDO. (рис.742)
2.В треугольнике ABC медианы BB1 и СС1 пересекаются в точке О. медиана ВВ1=15 см, СС1=18 см. угол BOC=90 найти периметр треугольника АВС.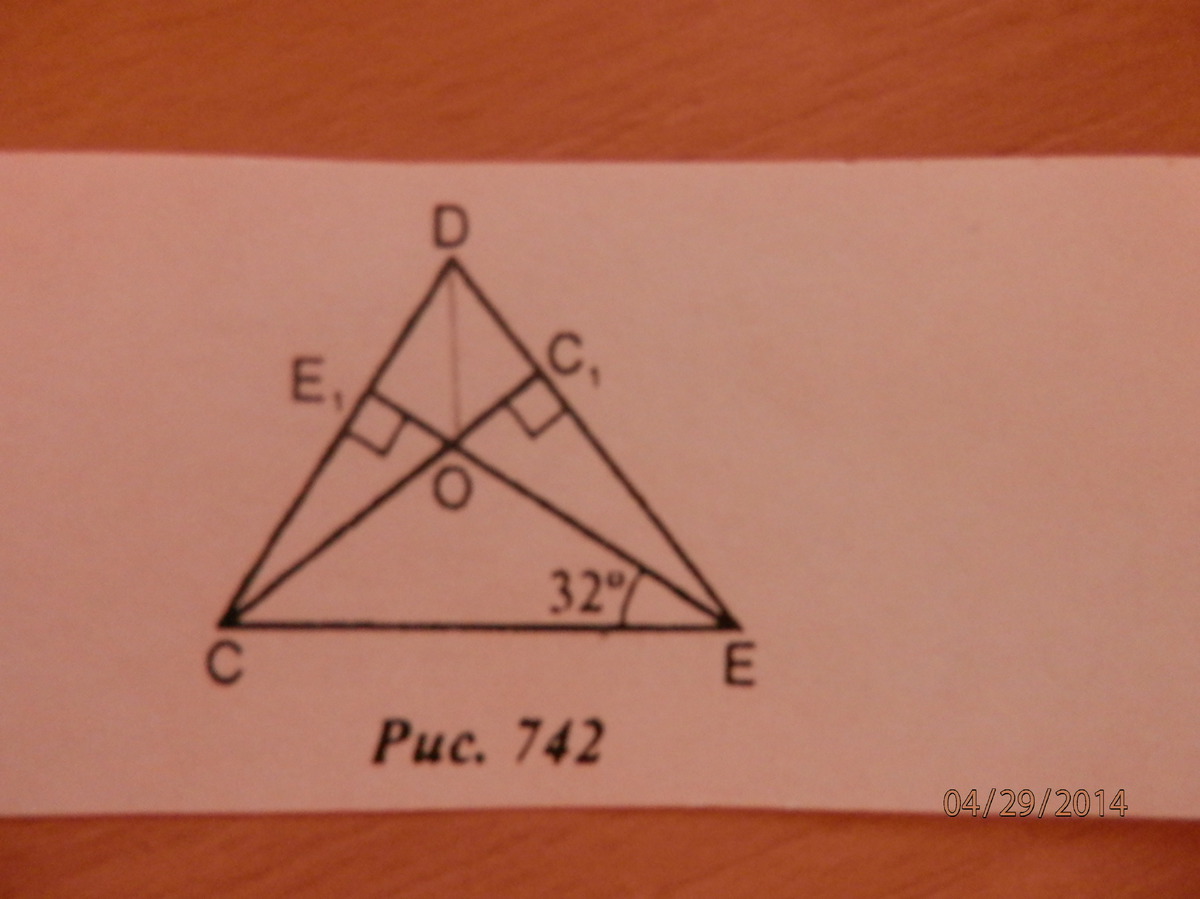
-
Предмет:
Геометрия -
Автор:
brodieki4k - 5 лет назад
-
Ответы 1
-
1. Высоты треугольника пересекаются в одной точке. => треугольник ЕОН прямоугольный и <EOH=90°-32°=58° (сумма острых углов =90°.<E1OD=58°, как вертикальный с <EOH.В прямоугольном треугольнике Е1ОD:<E1DO=90°-58°=32°.Или так: <CDH=<CEE1=32°, как углы с соответственно перпендикулярными сторонами.Ответ: <CDO=32°.2. ВВ1=15, СС1=18, <BOC=90°.Медианы точкой пересечения делятся в отношении 2:1, считая от вершины. Следовательно, С1О=(1/3)*СС1 = 6. ОС=12. В1О=5. ВО=10. Тогда ВС=√(ВО²+ОС²)=√(100+144)=√244=2√61.ВС1=√(ВО²+ОС1²)=√(100+36)=√136=2√34. АВ=2*ВС1=4√34.СВ1=√(СО²+ОВ1²)=√(144+25)=√169=13. АС=2*СВ1=26.Периметр треугольника АВС = 26+4√34+2√61.

-
Автор:
iris79 - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Нарисовать ребус к слове перог или завтрак
-
Предмет:
Русский язык -
Автор:
rocky28 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
как решить уравнение?
51k-47k=188-
Предмет:
Математика -
Автор:
ladislaomnaw - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
составить молекулярное, ионное и сокращенное ионное уравнение: а)Cu(OH)2+HCl=CuCl2+H2O
б)NaCO3+HaSO4=Na2SO4+H2O+CO2
в)Fe(OH)2+2HCl-
Предмет:
Химия -
Автор:
laurenhall - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
укажи какое правило надо помнить при написании указанных слов. лес, книжка, варежка, завод, гриб. 1 непроизносимая согласная.2 сомнительный согласный на конце и в середине слов. 3 проверяемая безударная гласная в корне слова. 4 непроверяемая безударная гласная в корне слова.
-
Предмет:
Русский язык -
Автор:
teodoracampos - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
