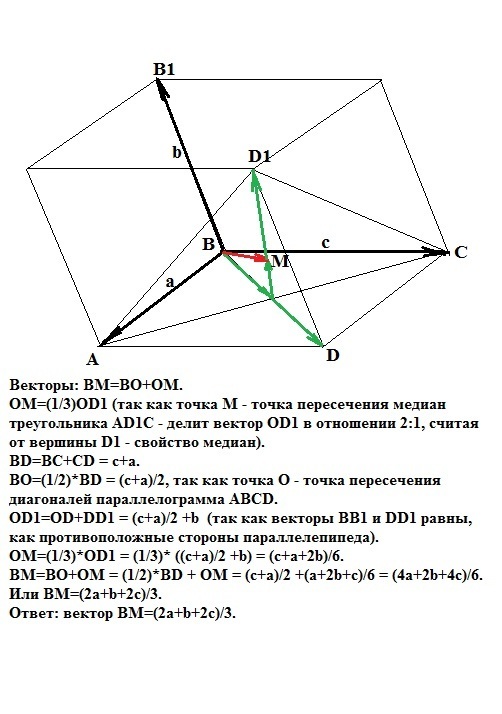
Дан параллелепипед ABCDA1B1C1D1.Медианы треугольника AСD1 пересекаются в точке M. Разложите вектор ВМ по векторам а = ВА, b= ВВ1, c = ВС.

Векторы: ВМ=ВО+ОМ.ОМ=(1/3)ОD1 (так как точка М - точка пересечения медиан треугольника AСD1 - делит вектор ОD1 в отношении 2:1, считая от вершины D1 - свойство медиан).BD=BC+CD = c+a.ВО=(1/2)*BD = (c+a)/2, так как точка О - точка пересечения диагоналей параллелограмма АВСD.OD1=OD+DD1 = (c+a)/2 +b  (так как векторы BB1 и DD1 равны, как противоположные стороны параллелепипеда).OM=(1/3)*OD1 = (1/3)* ((c+a)/2 +b) = (c+a+2b)/6.BM=BO+OM = (1/2)*BD + OM = (c+a)/2 +(a+2b+c)/6 = (4a+2b+4c)/6.Или ВМ=(2a+b+2c)/3.Ответ: вектор ВМ=(2a+b+2c)/3.