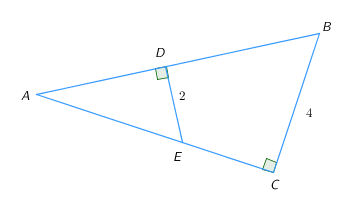
В прямоугольном треугольнике ABC из произвольной точки E катета AC опущен перпендикуляр EDна гипотенузу AB. DE=2, BC=4. Площадь треугольника ADE равна 5. Найдите площадь треугольника ABC.

 Находим ADисходя из площади и катета DE:5:2*2=5 Исходя из подобия тр-ков ABC и  EDA DE относится к DC как 2/4, т.е. как 1/2Следовательно AD относится к AC как 1/2Отсюда находим AC:5*2=10 Зная катеты тр-ка ABC: АС=10, ВС=4 находим площадь тр-ка (10*4)/2=40/2=20             Ответ: S=20