Из одной точки к окружности проведены две касательные. Длина каждой касательной 13 см, а расстояние между точками касания 24 см. Найти радиус окружности.

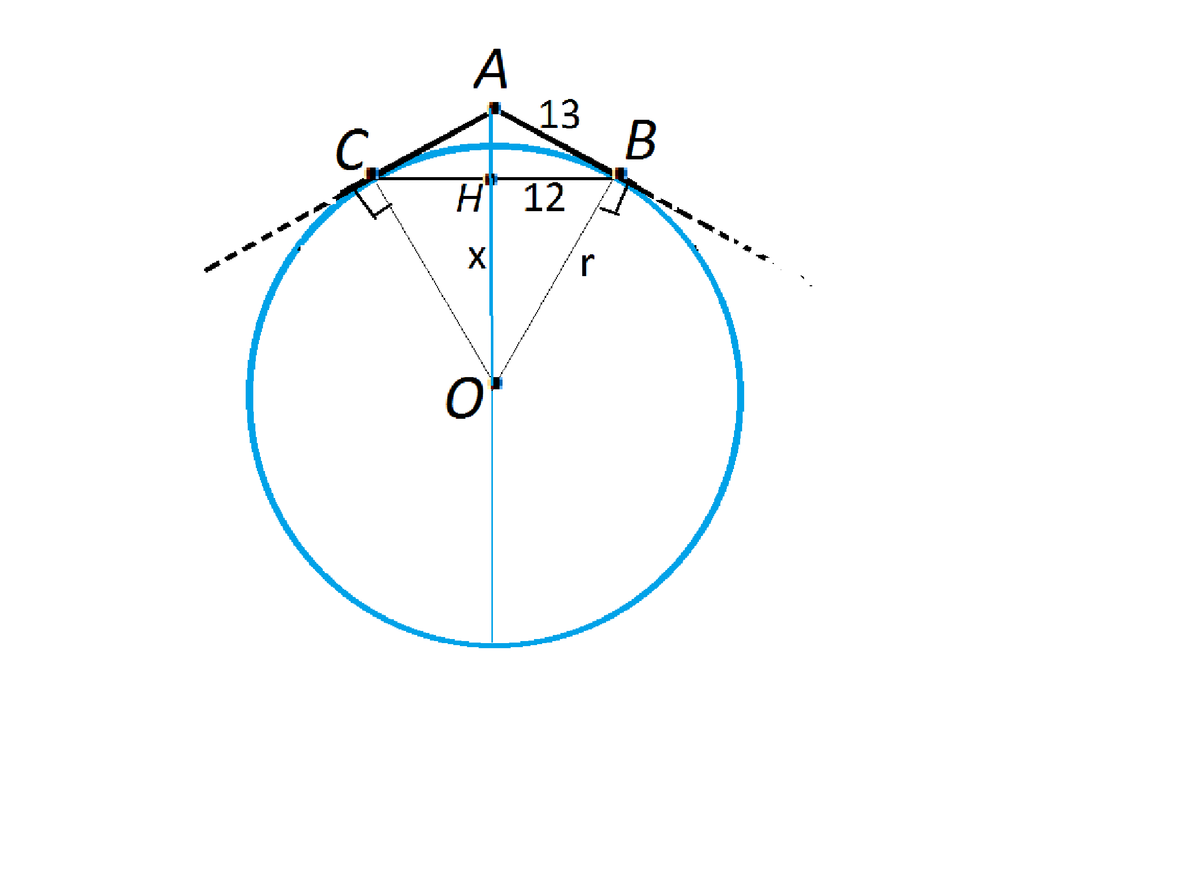
Сделаем и рассмотрим рисунок. Пусть касательные проведены из точки А, аС и В - точки касания.По условию АВ=АС=13ВС=24АВС - равнобедренный треугольник.Соединим А и центр О.Треугольник ВОС равнобедренный.АН - высота треугольника ВАС.ОН - высота треугольника ВОС.ВН=24:2=12Из ⊿АНВ по т.Пифагора находим АН=5OВ=rРассмотрим прямоугольный треугольник АВО.ОН в нем - высота.Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотойАН=5.ВН²=5 ОН144=5 ОНОН=28,8Из прямоугольного треугольника ВНО:ОВ²=ОН²+ВН²OB=rr²=28,8²+12²r²=829,44+144=973,44r=31,2 -----bzs@