-
помогите срочно,сидим на кр,хоть одно из того и того варианта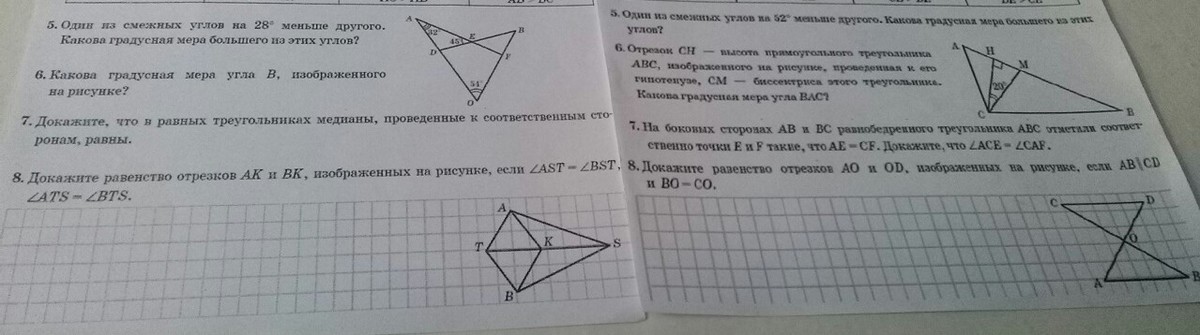
Ответы 4
-
2 ва риант
-
Автор:
kennyshort - 6 лет назад
-
0
-
-
2 еще
-
Автор:
karissa - 6 лет назад
-
0
-
-
спасибо
-
Автор:
banjocook - 6 лет назад
-
0
-
-
1.5) Сумма смежных углов равна 180°.Обозначим больший угол через х. Тогда: х + (х - 28) = 1802х - 28 = 1802х = 208х = 104°1.6) <BEF = <AED = 45°<AFO = 180° - <OAF - <AOF = 94°<AFB = 180° - <AFO = 86°<B = 180° - <BEF - <AFB = 49°1.7) Нарисуйте сами два равных треугольника: АВС и ЕFG. BD -- медиана ΔАВС, EH -- медиана ΔЕFG.Из равенства треугольников АВС и ЕFG следует: AB = EF, AD = EH, <A = <E.Тогда ΔABD = ΔEFH.Из равенства треугольников следует равенство соответствующих сторон: BD = FH, т. е. медианы равны.1.8) ΔTAS = ΔTBS по стороне и двум прилегающим углам:TS -- общая, <ATS = <BTS, <AST = <BST.Тогда равны соотвествующие стороны: АТ = ВТ.Из этого следует равенство треугольников: ΔАТК = ΔВТК по двум сторонам и углу между ними: АТ = ВТ, ТК -- общая, <ATS = <BTS.Из равенства ΔАТК = ΔВТК следует равенство сторон: АК = ВК.2.5) Сумма смежных углов равна 180°.Обозначим больший угол через х. Тогда: х + (х - 52) = 1802х - 52 = 1802х = 232х = 116°2.6) <ACM = 90/2 = 45°<ACH = <ACM - 20° = 25°<BAC = 180 - 90 - <ACH = 65°2.7) ΔAEC = ΔCFA по двум сторонам и углу между ними: АС -- общая, AE= CF, <BAC = <DCA. Из равенства треугольников следует равенство соответствующих углов: <ACE = <CAF.2.8) ΔAOB = ΔDOC по стороне и двум прилегающим к ней углам: ВО = СО, <AOB = <DOC как вертикальные, <OBA = <OCD как накрест лежащие.Из равенства треугольников следует равенство соответствующих сторон: АО = OD.
-
Автор:
blancheimtb - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
К каким явлениям относится: ЭХО, Звезды мерцают?
Явления; звуковое, тепловое, механическое, световое, электрическое-
Предмет:
Физика -
Автор:
dominicrussell - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
материк на котором находится наша страна Россия называют
-
Предмет:
Другие предметы -
Автор:
pookie - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
описати дерево каштан
-
Предмет:
Українська мова -
Автор:
tiger48 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
(9 12/25 - 8 16/25)- 4 17/25=?
-
Предмет:
Математика -
Автор:
lorenzobjnj - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
