Задать вопрос Регистрация
Помочь другим

  • Найдите на оси у  точку, равноудалённую от точек А(-3; 7; 4) и В(2; -5; -1)

    Помогите, пожалуйста :)

     

     

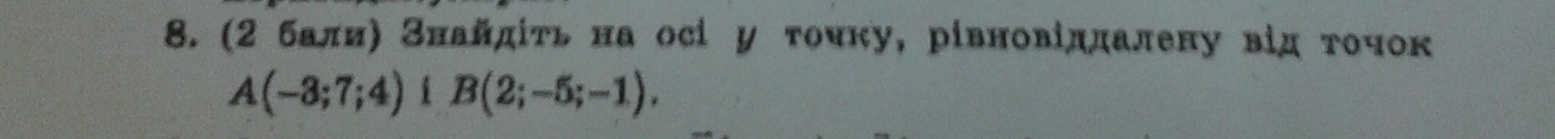
    question img

Ответы 2

  • А(-3; 7; 4) 

    В(2; -5; -1)

    Точка С лежит на оси ОУ, значит С(0;у;0) и |AC|=|BC|

    Вектор АС(0-(-3);у-7;0-4)=(3;у-7;-4)

    |AC|=\sqrt{3^{2}+(y-7)^{2}+(-4)^{2}}=\sqrt{25+(y-7)^{2}}

     

    Вектор ВС(0-2;у+5;0-(-1))=(-2;у+5;1)

    |DC|=\sqrt{(-2)^{2}+(y+5)^{2}+1^{2}}=\sqrt{5+(y+5)^{2}}

     

    |AC|=|BC|

    \sqrt{25+(y-7)^{2}}=\sqrt{5+(y+5)^{2}}

    25+(y-7)^{2}=5+(y+5)^{2}

    25+y^{2}-14y+49=5+y^{2}+10y+25

    24y=44

    y=1\frac{5}{6}

     

    C(0; 1 5/6; 0)

     

     

     

    • Автор:

      alia
    • 5 лет назад
    • 0

  • если мы ищем на оси точку, то значит две другие координаты будут равны 0.

    С(0;y;0)

    |AC| = |BC|

    AC = \sqrt{3^{2} + (y-7)^{2} + (-4)^{2}}

    BC = \sqrt{(-2)^{2} + (y+5)^{2} + (1)^{2}}

    если равны корни, то и равны подкоренные выражения:

    3^{2} + (y-7)^{2} + (-4)^{2} = (-2)^{2} + (y+5)^{2} + (1)^{2}

    (y-7)^{2} + 25 = (y+5)^{2} + 5

    (y-7)^{2} - (y+5)^{2} = -20

    ((y-7) - (y+5)) * ((y-7)+(y+5))  = -20

    -12*(2y-2)=-20

    24y=44

    [tex]y=\frac{44}{24}[\tex]

     

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years