прямая. АВ. разбивает плоскость на две полуплоскости . из точек А и В в разные полуплоскости проведены равные отрезки АД и ВС причём <ВАД =<АВС какие из высказываний верны
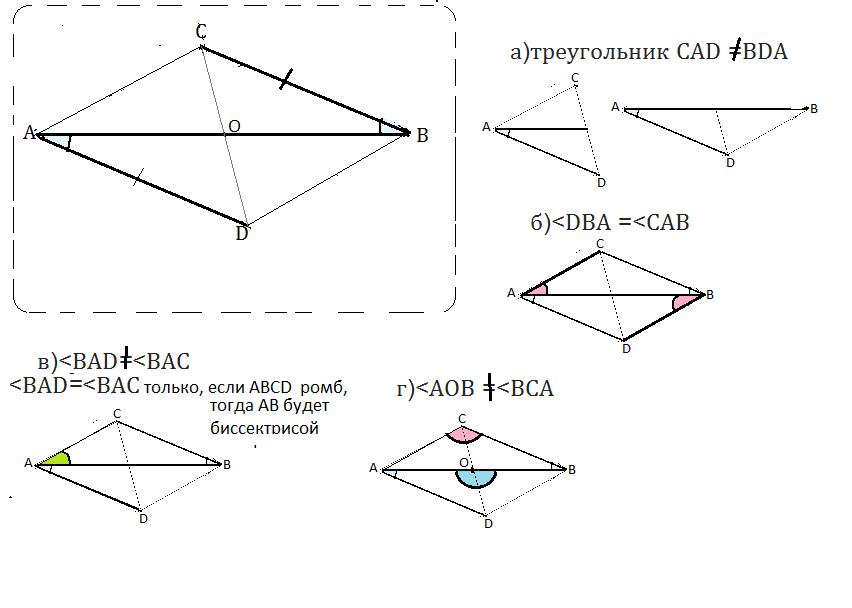
а)треугольник САД =ВДА
б)<ДВА =<САВ
в)<ВАД=<ВАС
г)<АОВ =<ВСА

Прямая АВ - секущая при ВС и АД. При этом равные по условию ∠ВАД=∠АВС - внутренние накрестлежащие.  Признак параллельных прямыхЕсли внутренние накрест лежащие углы равны, то прямые параллельны.⇒ АД параллельна ВС.Соединим А и С, Д и В.В четырехугольнике АВСД стороны АД и ВС  параллельны и по условию равны. Если противоположные стороны четырехугольника равны и параллельны,  этот четырехугольник - параллелограмм. а )треугольник САД  может быть  равен ВДА только если  четырехугольник АВСД - квадрат. б)∠ДВА =∠САВ как накрестлежащие при параллельных ВД и АС и секущей АВ.в) ∠ВАД=∠ВАС только в том случае, если АВСД - ромб.г)  если О - точка пересечения СД и АВ, угол АОВ - развернутый и не может быть равен углу ВСА.