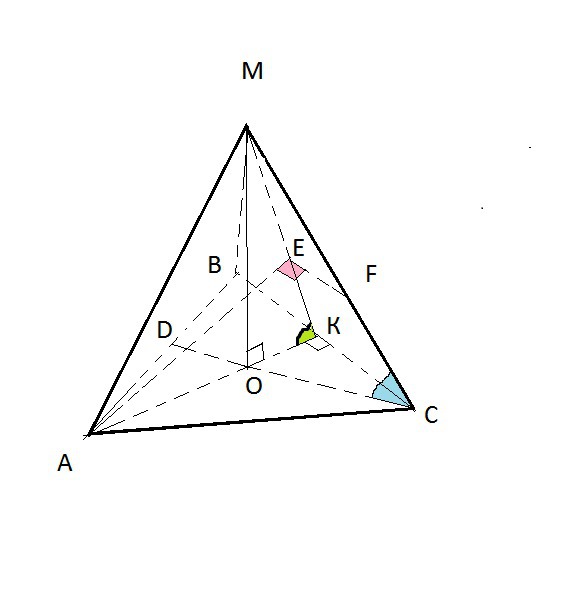
Точка M равноудалена от всех сторон правильного треугольника ABC ,сторона которого равна 4 см. Расстояние от Точки M до плоскости ABC равно 2см.
1)Докажите, что плоскость AMO перпендикулярна плоскости BMC(O-основание перпендикуляра, опущенного из M на плоскость ABC)
2)Найдите угол между плоскостью BMC и плоскостью ABC.
3)Найдите угол между MC и плоскостью ABC.

Cм. рисунок в приложенииВ основании пирамиды равносторонний треугольник АВС:АВ=ВС=АС=4 см.В равностороннем треугольнике все высоты равны.Высоты являются одновременно медианами и биссектрисами.МО ⊥ пл. АВС.ОА=ОВ=ОС=R ( радиус описанной окружности).R=a√3/3, где а- сторона правильного треугольника.ОА=ОВ=ОС=4√3/3ОК=OD=r ( радиус вписанной окружности).Медианты в точке пересечения делятся в отношении 2:1, считая от вершины.r=R/2=2√3/3Равные проекции имеют равные наклонные.МА=МВ=МС.а) АК- высота, медиана и биссектриса Δ АВС.АК⊥ВСВК=КС.МК⊥BC  по теореме о трех перпендикулярах ( проеция МК- ОК, ОК⊥ВС, так как АК ⊥ ВС).ВС ⊥ АК и ВС⊥ МКВС ⊥ двум пересекающимся прямым плоскости АМК, значит по признаку перпендикулярности прямой и плоскости, ВС ⊥ пл. АМК, а значит и пл. АМО.Чтобы найти линейный угол двугранного угла между плоскостями АМО (АМК) и ВМС, надо провести перпендикуляры к линии их пересечения.Линией пересечения является МК.Проводим АЕ⊥МК и ЕF║ВС. (ВС⊥МК ⇒ ЕF⊥MK).б) Угол между плоскостями АВС и МВС. Линией пересечения плоскостей является сторона ВС.АК⊥ВСМК⊥ВСУгол МКА - линейный угол двугранного угла.Из прямоугольного треугольника МОКtg ∠МКО=MO/OК=2/(2√3/3)=√3 ∠МКО=60°в) угол между прямой МС и плоскостью АВС - угол между прямой и её проекцией на эту плоскость.Проекцией МС на плоскость АВС является ОС.Из прямоугольного треугольника МОСtg∠MCO=MO/OC=2/(4√3/3)=√3/2∠MCO=arctg (√3/2).