-
в паскале или блок схему,но лучше в паскале
ваще не шарю-.-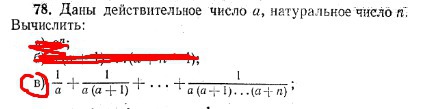
-
Предмет:
Информатика -
Автор:
melchor - 6 лет назад
-
Ответы 1
-
В подобных формулах, когда присутствует некоторое количество слагаемых, каждое из которых состоит из некоторого количества сумм или произведений, проще всего, конечно, использовать рекурсивные функции. Это позволяет писать программы быстро и кратко, но расплатой бывает быстрое переполнение программного стека при росте глубины рекурсии и длительное время счёта. Эффективнее, особенно при значительном количестве слагаемых, использовать итерацию, для чего первоначальное выражение следует немного преобразовать.
var a,p,s:real; n,i:integer;begin Write('a='); Read(a); Write('n='); Read(n); p:=1/a; s:=p; for i:=1 to n do begin p:=p/(a+i); s:=s+p end; Writeln('S=',s)end.Примерa=2n=5S=0.718253968253968
-
Автор:
gordo1hwo - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
как объяснить ребенку что такое диаграмма?
-
Предмет:
Математика -
Автор:
silly gillymrq3 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Произведение ( Беркут и Тугар Вовк ) що сподобалось і не сподобалось .
-
Предмет:
Українська література -
Автор:
brendonc16a - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
найдите в стихотворении Г.Сапгира слова с пройденными буквосочетаниями
-
Предмет:
Русский язык -
Автор:
aureliogomez - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите с домашним заданием!Раскрой смысл арабской пословицы "Люди больше похожи на своё время, чем на своих отцов" Подумай, чем отличается жизнь общества...
-
Предмет:
Обществознание -
Автор:
bobby47 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
