-
Как построить логическое выражение по таблице истинности?
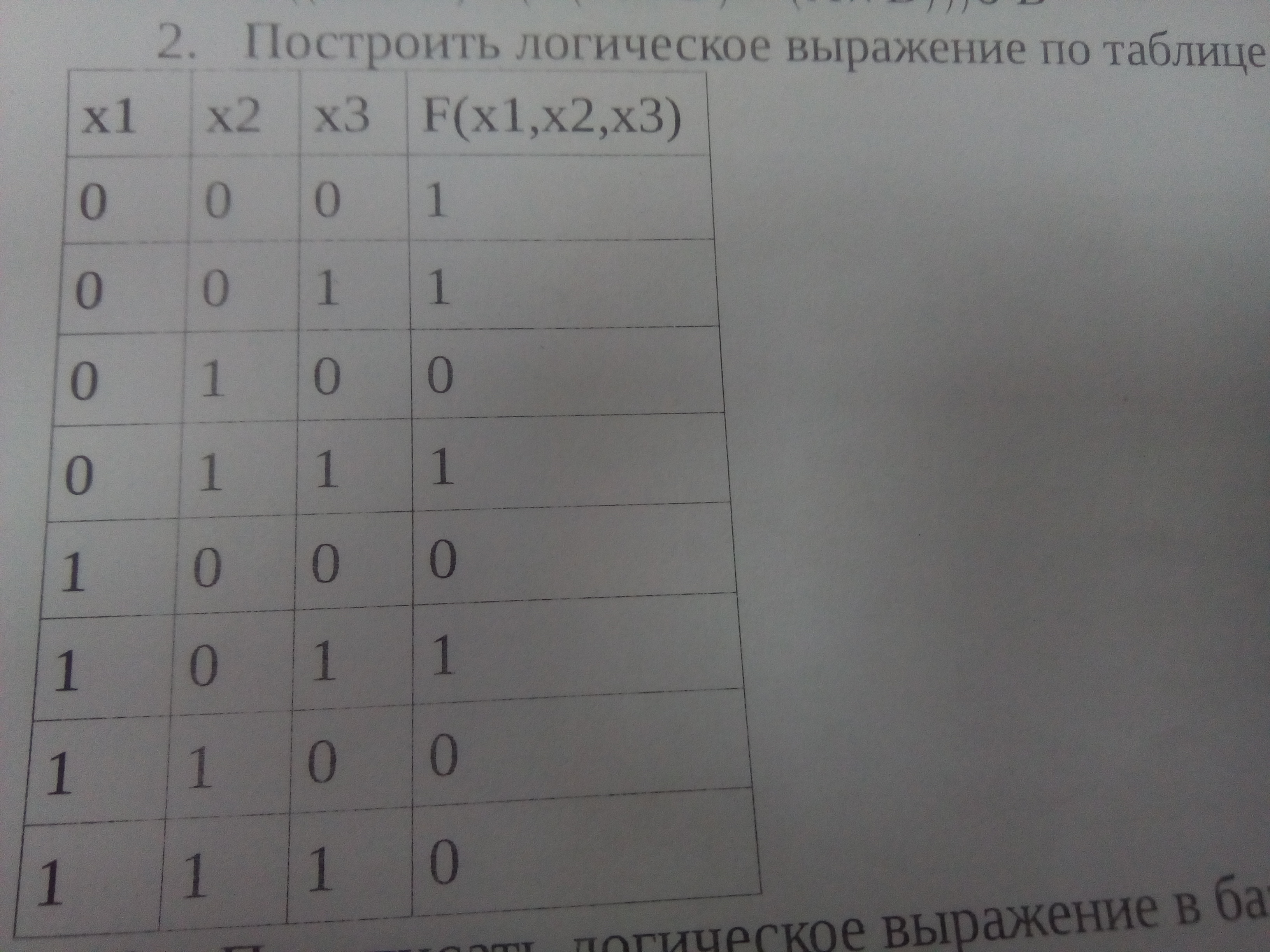
-
Предмет:
Информатика -
Автор:
jaydinrocha - 6 лет назад
-
Ответы 1
-
Смотрим, каких строк больше - с единицей в конечной функции F или с нулём. Тут поровну и поступаем, как для случая, когда единичных значений больше.Выписываем строки с единицами и соединяем их по ИЛИF = 000 ∨ 001 ∨ 011 ∨ 101Заменяем нули на значения переменных с отрицанием, а единицы - просто на значения переменных.F = ¬x₁¬x₂¬x₃ ∨ ¬x₁¬x₂x₃ ∨ ¬x₁x₂x₃ ∨ x₁¬x₂x₃Это выражение можно упростить, но для этого удобнее перейти к другой системе обозначений, заменяя отрицание (¬) надчеркиванием, а дизъюнкцию (∨) знаком сложения (+). Мы не ставили между переменными знак конъюнкции (& или ∧), чтобы излишне не загромождать запись, но должны понимать, что ¬x₁¬x₂¬x₃ - это на самом деле запись выражения¬x₁ ∧ ¬x₂ ∧ ¬x₃
Если бы нулевых строк с таблице было больше, удобнее было бы выписать все нулевые, а потом перед всем полученным выражением поставить общий знак отрицания.
-
Автор:
carolinefjz3 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Молот масою 2 кг, що рухається зі швидкістю 5 м/с, вдаряє по цвяху й забиває його в дошку на 8 мм.визначіть силу опору деревини
-
на познание мира мне очень нужно сообщение на тему(состояние озера Балхаш).
пожалуйста помогите написать надо по детскому.
пожалуйста дам 10 баллов.-
Предмет:
Окружающий мир -
Автор:
ace61 - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
какие сельские орудия труда появились при Петре 1
-
Предмет:
Английский язык -
Автор:
mariolowe - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
За первые 2ч 60км/ч за вторые 2ч 40км/ч найти среднюю скорость Мотоцикла
С решением!)
How much to ban the user?
1 hour
1 day
100 years
