-
1. На фото
2. Определите количество натуральных чисел, меньших 200.10 (10-система счисления), для которых выполняется условие: в записях числа в шестеричной и двенадцатеричной системах счисления в младшем разряде стоит цифра 3. В ответе запишите целое число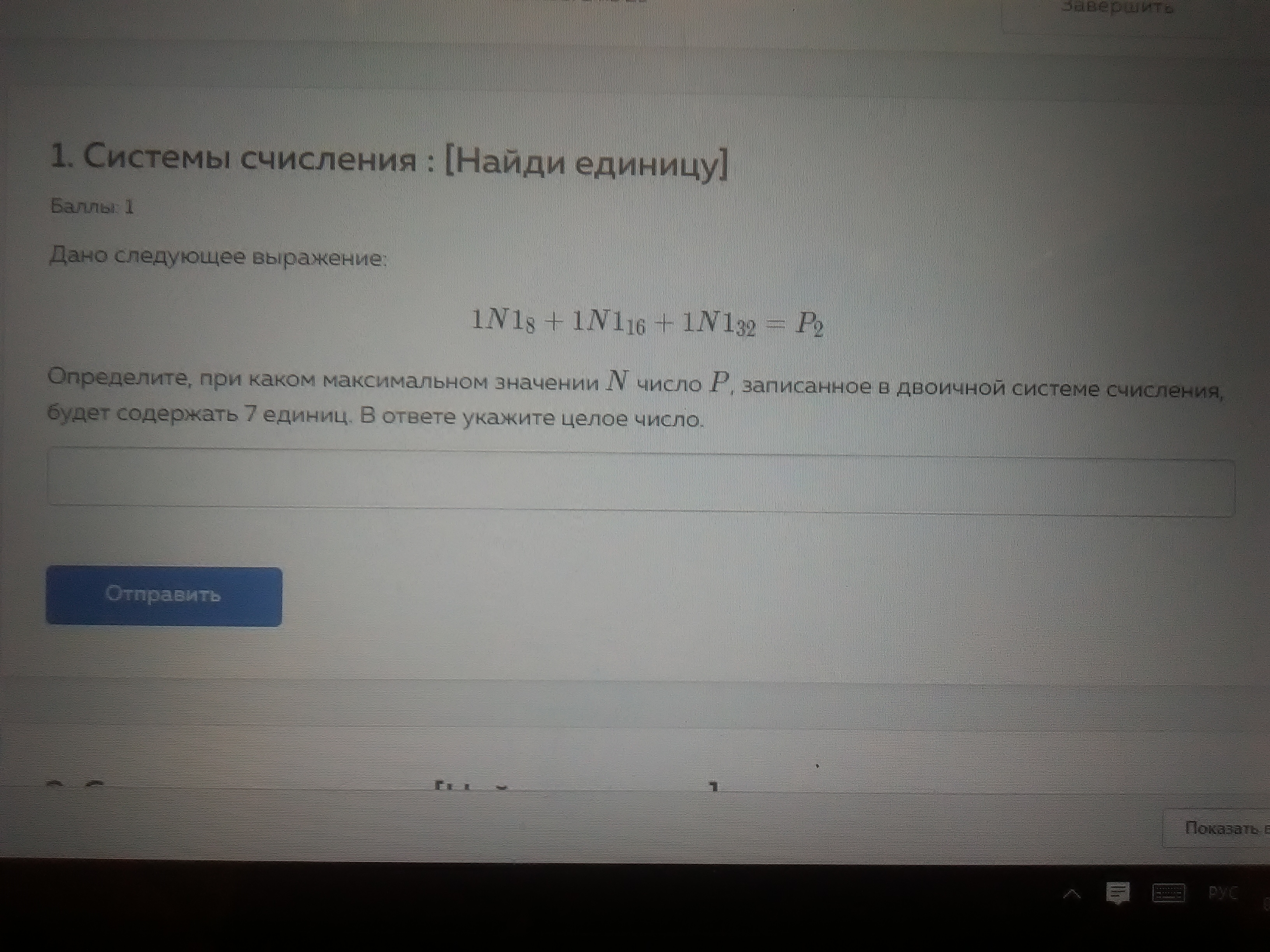
-
Предмет:
Информатика -
Автор:
brewsterh276 - 6 лет назад
-
Ответы 2
-
То есть надо найти количество чисел от 1 до 200, которые при делениина 6 и на 12 дают остаток 3.n:=0;for i:=1 to 200beginif (i mod 6 = 3) and (i mod 12 = 3) then n := n + 1;end;write n;end.
-
Автор:
marley41 - 6 лет назад
-
0
-
-
Ответ:
1) N=7; 2) 17 чисел
Объяснение:
1) В 8-ной системе не может быть цифры больше 7.
Возьмём N=7.
171(8) + 171(16) + 171(32) = 8^2+7*8+1+16^2+7*16+1+32^2+7*32+1 = 1739
Переведем 1739 в двоичное число.
1739 = 1*1024+1*512+0*256+1*128+ 1*64+0*32+0*16+1*8+0*4+1*2+1 = 11011001011(2)
Как видим, в этом двоичном числе ровно 7 единиц.
N = 7.
2) Эта задача по сути означает следующее: нужно найти количество чисел меньше 200(10), которые при делении на 6 и на 12 дают остаток 3.
Это числа: 3, 15, 27, 39, 51, 63, 75, 87, 99, 111, 123, 135, 147, 159, 171, 183, 195.
Всего 17 чисел.
-
Автор:
coy - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Из чего состоит вода 3 класс
-
Предмет:
Другие предметы -
Автор:
carolyn - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
срочно Олимпиада по английскому языку задание на фото слова которые надо будет ставить я напишу даю достаточно много баллов если всё выполните правильно Я на вас подпишусь пролайкаю все ваши ответы и назову ваш ответ лучший
Вот и эти слова
together
the pan
daughter
the cooker
pizza
granddaughter
эти слова надо вставить в те предложения-
Предмет:
Английский язык -
Автор:
clotildeellis - 6 лет назад
-
Ответов:
7 -
Смотреть
-
-
273321:9 в столбик
Пожалуйста помогите-
Предмет:
Математика -
Автор:
gooberg8uz - 6 лет назад
-
Ответов:
0 -
Смотреть
-
- Закончить уравнения реакции: CH2=CH-CH3+Hl2
How much to ban the user?
1 hour
1 day
100 years
