-
Путем тождественных преобразований определить, на каких наборах данных логическая функция принимает значение 1. Хочу понять как это делается
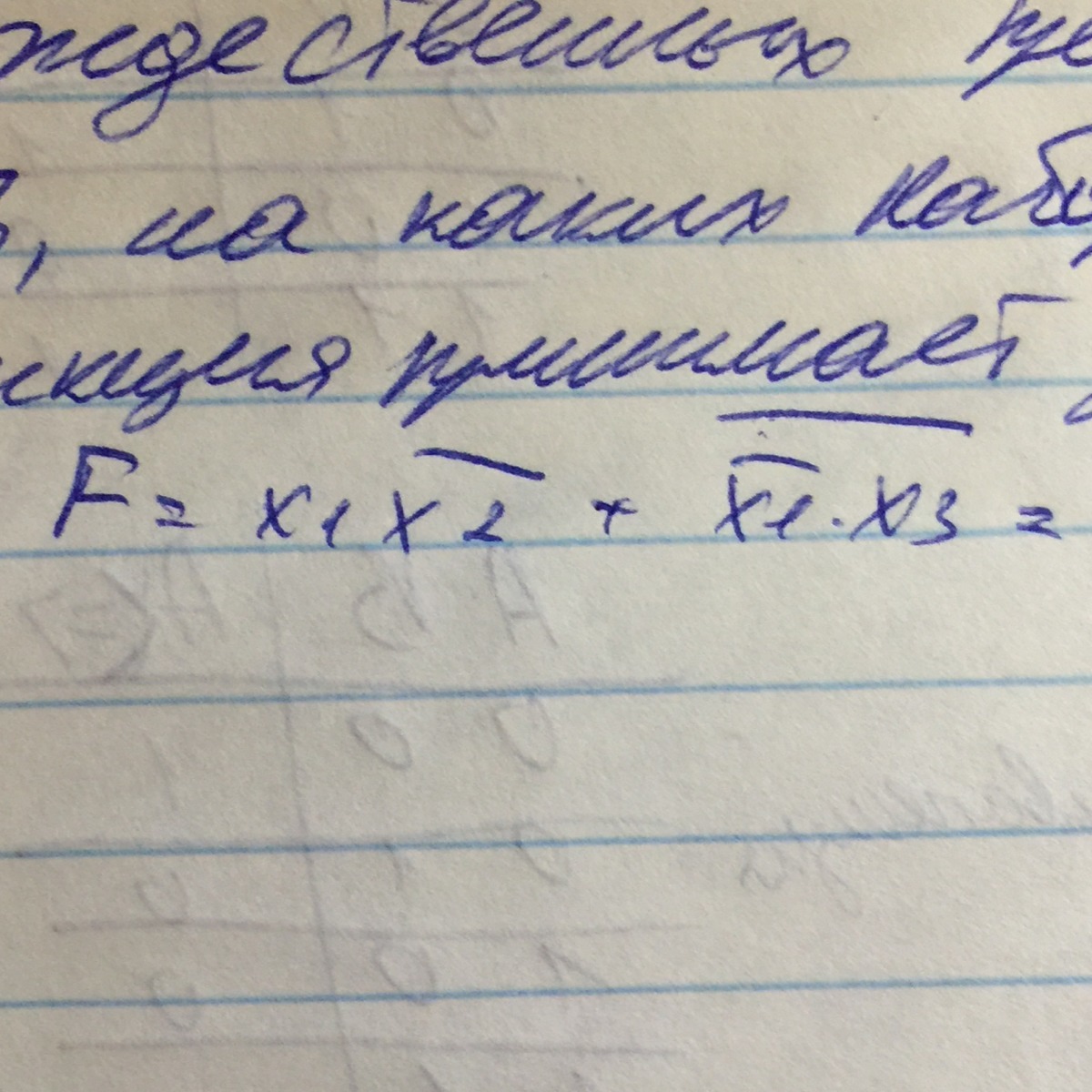
-
Предмет:
Информатика -
Автор:
jakaylatanner - 6 лет назад
-
Ответы 5
-
я извиняюсь, куда над Х2 палка подевалась????
-
Автор:
davispgub - 6 лет назад
-
0
-
-
Потерялась:( Хотя роли это не сыграло: !х2+1 тоже =1
-
Автор:
golden - 6 лет назад
-
0
-
-
А вот обозначение F=x2+1 это нехорошо
-
Автор:
lucascarter - 6 лет назад
-
0
-
-
(инверсию/отрицание обозначаю !)Сначала преобразуем, используя правила деМоргана и др.: х1•!х2+(х1+!х3)= х1•(!х2+1)+ !х3= х1+!х3= !(!х1•х3) -от х2 не зависит, поэтому из 8 наборов в таблице истинности осталось 4: х1х3= 00 01 10 11, подставляем и находим F= 1 0 1 1, т.е. F=1 на наборах 00 10 11 двоичных переменных х1, х3
-
Автор:
jaiden6tam - 6 лет назад
-
0
-
-
Вначале преобразуем второе слагаемое по закону де-Моргана. Потому что первое слагаемое никак нельзя упростить.
Получаем выражение, с которым можно обращаться по законам обычной алгебры
Дизъюнкция истинна всегда, кроме случая, когда оба значения переменных ложны, поэтому достаточно чтобы или x₁=1, или x₃=0. Или и то и другое одновременно.
Это реализуется для наборов x₁x₃ = 00 10 11 для любых x₂
-
Автор:
bustercjet - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Найдите натуральное число удовлетворяющее неравенству 1,5<2 1/6-х/8<1 7/12
-
Предмет:
Математика -
Автор:
malachi576 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
___we work___we earn 1 many, many 2 the most, the most3 much, much 4 the more, the more
-
Предмет:
Английский язык -
Автор:
oscarc0nt - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Используя только неорганические вещества и катализаторы, предложите метод получения CH3COOCH из CH3CH2CH2CH3. Напишите уравнения химических реакций с указанием условий их проведения.
-
Предмет:
Химия -
Автор:
mr kittynolan - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- В заданной схеме превращений C O 2 X −→ C a C O 3 Y → C O 2 веществами X и Y соответственно являются: 1. Ca 2. CaO 3. H2O 4. HCl 5. H2S
How much to ban the user?
1 hour
1 day
100 years
