-
Работа с таблицей истинности по информатике. Решите пожалуйста!
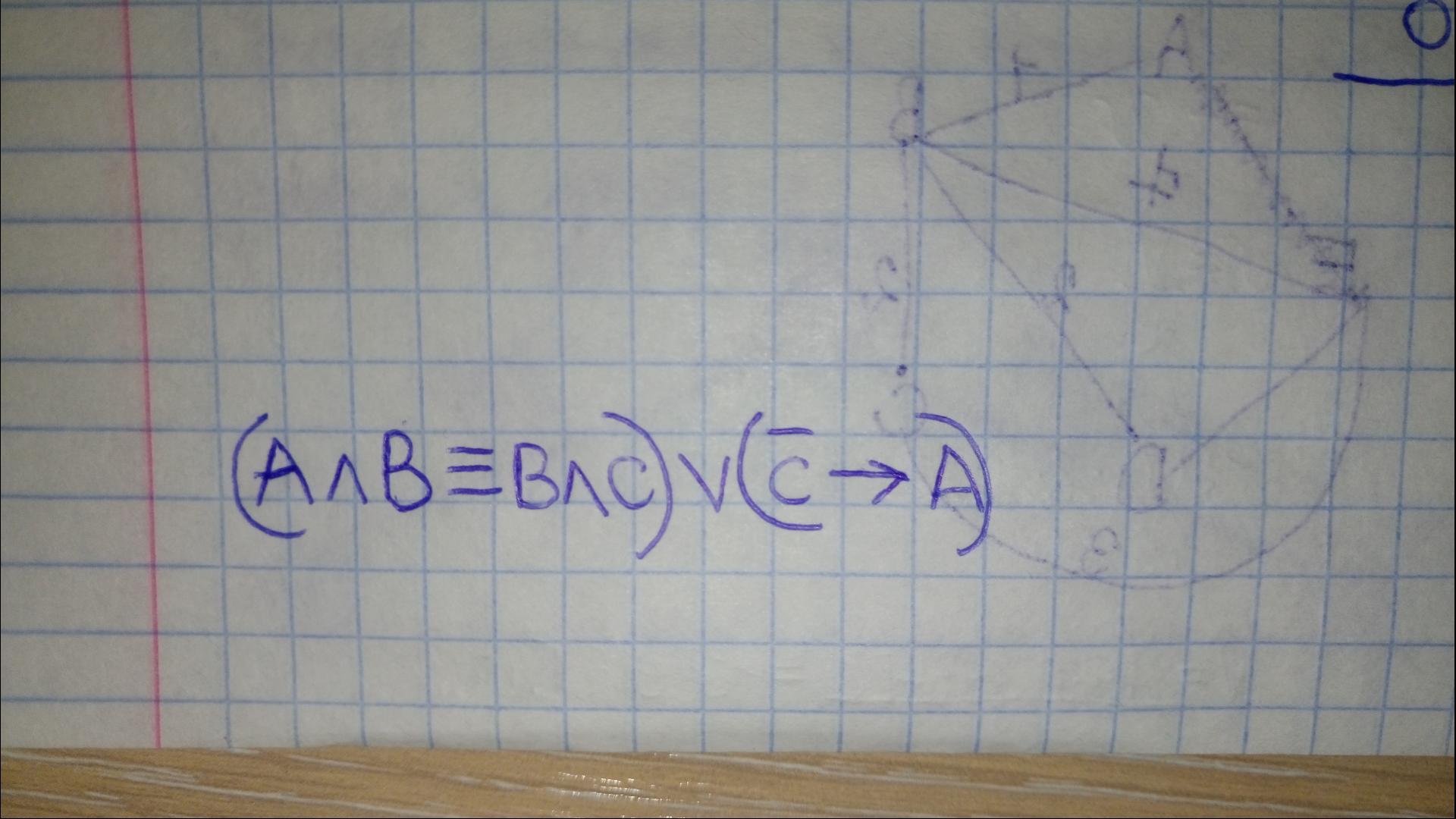
-
Предмет:
Информатика -
Автор:
carsonross - 6 лет назад
-
Ответы 1
-
Ответ:
При любых A, B и C данное выражение истинно.
Объяснение:Для начала упростим эквивалентность и импликацию.
Экивалентность (≡) раскрывается вот так:
x ≡ y = x ∧ y ∨ -x ∧ -yПрименим к нашим данным:
A ∧ B ≡ B ∧ C = (A ∧ B ∧ B ∧ C) ∨ ( -(A ∧ B) ∧ -(B ∧ C) ) =
Первая скобка упрощается по закону повторения (B ∧ B = B), а вторая скобка, а точнее отрицание раскрывается по закону де Моргана:
= (A ∧ B ∧ C) ∨ ( -A ∨ -B ∧ -B ∨ -C) =
По закону исключения третьего (A ∨ -A = 1) упрощаем запись:
= 1
На самом деле я здесь очень сильно упростил запись. На самом деле нам не помешало бы раскрыть данную дизъюнкцию, "перемножив" A на -A, A на -B, A на -C, B на -A и так далее. Но в итоге данная запись сократится в единицу.
Теперь рассмотрим импликацию (⇒):
(x ⇒ y) = -x ∧ yПрименим к нашим данным:
(-C ⇒ A) = -(-C) ∧ A =
По закону двойного отрицания (-(-C) = C):
C ∧ A
Итого наш пример принял такой вид:
1 ∨ C ∧ A
Данное выражение всегда истинно, поскольку дизъюнкция истинна в том случае, когда одно из выражений истинно, а в нашем случае левая часть (единица), то есть дизъюнкция вседа истинна.
-
Автор:
samantha15 - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Б.Васильев '' Экспонат'' написать сочинение '' о чем я задумался после прочтения''
-
Предмет:
Литература -
Автор:
giana - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Водонапорный бак расположен на h=90 м. Определите давление воды в кране на вашем дачном участке. Почему это давление вечером ниже, чем днем?
РЕШИТЕ ПЛЗ СРОЧНО!!!!
Даю 70 баллов -
Срочно помогите решить задания по английскому!!!
Заранее спасибо.-
Предмет:
Английский язык -
Автор:
walkerlang - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Прочитайте отрывок из рассказа «Рождество» В. В. Набокова.
Составьте его сложный план, описывая действия и мысли героя.
Охарактеризуйте душевное состояние героя рассказа.
Когда на следующее утро, после ночи, прошедшей в мелких нелепых снах, вовсе не
относившихся к его горю, Слепцов вышел на холодную веранду, так весело выстрелила под
ногой половица, и на беленую лавку легли райскими ромбами отраженья цветных стекол.
Дверь поддалась не сразу, затем сладко хряснула, и в лицо ударил блистательный мороз.
Песком, будто рыжей корицей, усыпан был ледок, облепивший ступени крыльца, а с выступа
крыши, остриями вниз. свисали толстые сосули, сквозящие зеленоватой синевой. Сугробы
подступали к самым окнам флигеля, плотно держали в морозных тисках оглушенное
деревянное строеньице. Перед крыльцом чуть вздувались над гладким снегом белые купола
клумб, а дальше сиял высокий парк, где каждый черный сучок окаймлен был серебром, и
елки поджимали зеленые лапы под пухлым и сверкающим грузом.
Слепцов, в высоких валенках, в полушубке с каракулевым воротником, тихо зашагал
по прямой, единственной расчищенной тропе в эту ослепительную глубь. Он удивлялся, что
еще жив, что может чувствовать, как блестит снег, как ноют от мороза передние зубы. Он
заметил даже, что оснеженный куст похож на застывший фонтан, и что на склоне сугроба -
песьи следы, шафранные пятна, прожегшие наст. Немного дальше торчали столбы мостика, и
тут Слепцов остановился. Горько, гневно столкнул с перил толстый пушистый слой. Он сразу
вспомнил, каким был этот мост летом. По склизким доскам, усеянным сережками, проходил
его сын, ловким взмахом сачка срывал бабочку, севшую на перила. Вот он увидел отца.
Неповторимым смехом играет лицо под загнутым краем потемневшей от солнца соломенной
шляпы, рука теребит цепочку и кожаный кошелек на широком поясе, весело расставлены
милые, гладкие, коричневые ноги в коротких саржевых штанах, в промокших сандалиях.
Совсем недавно, в Петербурге, - радостно, жадно поговорив в бреду о школе, о велосипеде, о
какой-то индийской бабочке, - он умер, и вчера Слепцов перевез тяжелый, словно всею
жизнью наполненный гроб, в деревню, в маленький белокаменный склеп близ сельской
церкви.
Было тихо, как бывает тихо только в погожий, морозный день. Слепцов, высоко подняв
ногу, свернул с тропы и, оставляя за собой в снегу синие ямы, пробрался между стволов
22
удивительно светлых деревьев к тому месту, где парк обрывался к реке. Далеко внизу, на
белой глади, у проруби, горели вырезанные льды, а на том берегу, над снежными крышами
изб, поднимались тихо и прямо розоватые струи дыма. Слепцов снял каракулевый колпак,
прислонился к стволу. Где-то очень далеко кололи дрова,- каждый удар звонко отпрыгивал в
небо,- а над белыми крышами придавленных изб, за легким серебряным туманом деревьев,
слепо сиял церковный крест.
Критерии оценивания Дескриптор Балл
Обучающийся
Составляет сложный план
отрывка из произведения
делит текст на основные смысловые части;
озаглавливает их (пункты плана);
1
делит на смысловые части содержание каждого
пункта и озаглавливает (подпункты плана);
1
оформляет план в соответствие с
грамматическими нормами.
1
Характеризует героев
произведения на основе
деталей и цитат из текста
выделяет важные для характеристики героя
детали;
1
анализирует и истолковывает детали, создающие
образ главного героя;
1
делает выводы о характере героя;
эмоционально выражает свое отношение к
поведению героя и его системе ценностей;
1
использует цитаты из текста для подтверждения
своих мыслей.
1
Всего баллов 7
ПРОШУ НАПИСАТЬ СВОЕ НЕ ОТКУДА НЕ КОПИРОВАТЬ. ПРОВЕРЯЮ- ЗА КОПИРОВАННОЕ НЕ ПОСТАВЛЮ ОЦЕНКУ-
Предмет:
Литература -
Автор:
barneybell - 6 лет назад
-
Ответов:
6 -
Смотреть
-
