Эух. Нужна помощь в составлении математических моделей и блок-схем. Программа паскаль. Буду рад, если поможете с любой из списка.

Повторяю, что решение задач в паскале у меня есть, мне нужны именно Блок-схемы и математическое решение. (можно в тетради)

1. Вычислить длину окружности и площадь круга одного и того же заданного радиуса R.

2. Вычислить площадь и периметр правильного N-угольника, описанного около окружности R(Рассмотреть N- целого числа, R- вещественного типа)


Для каждой задачи составить программу, выводящее значение правда/ложь.

3. Треугольник со сторонами a, b, c является равнобедренным.

4. Данное четврехзначное число читается одинаково слева направо и справа налево.

5. Заданы координаты трех точек плоскости. Эти точки не лежат на одной прямой.


Для каждой задачи составить программу с ветвящейся структурой, используя условный оператор IF.

6. Грузовой автомобиль выехали одного города в другой со скоростью v1 км/ч. Через t ч в этом же направлении выехал легковой автомобиль со скоростью v2 км/с. Составить программу, определяющую, догонит ли легковой автомобиль грузовой через t1 после своего выезда.

7. Написать программу, которая по заданным трём числам определяет, является ли сумма каких-либо двух из них положительной.

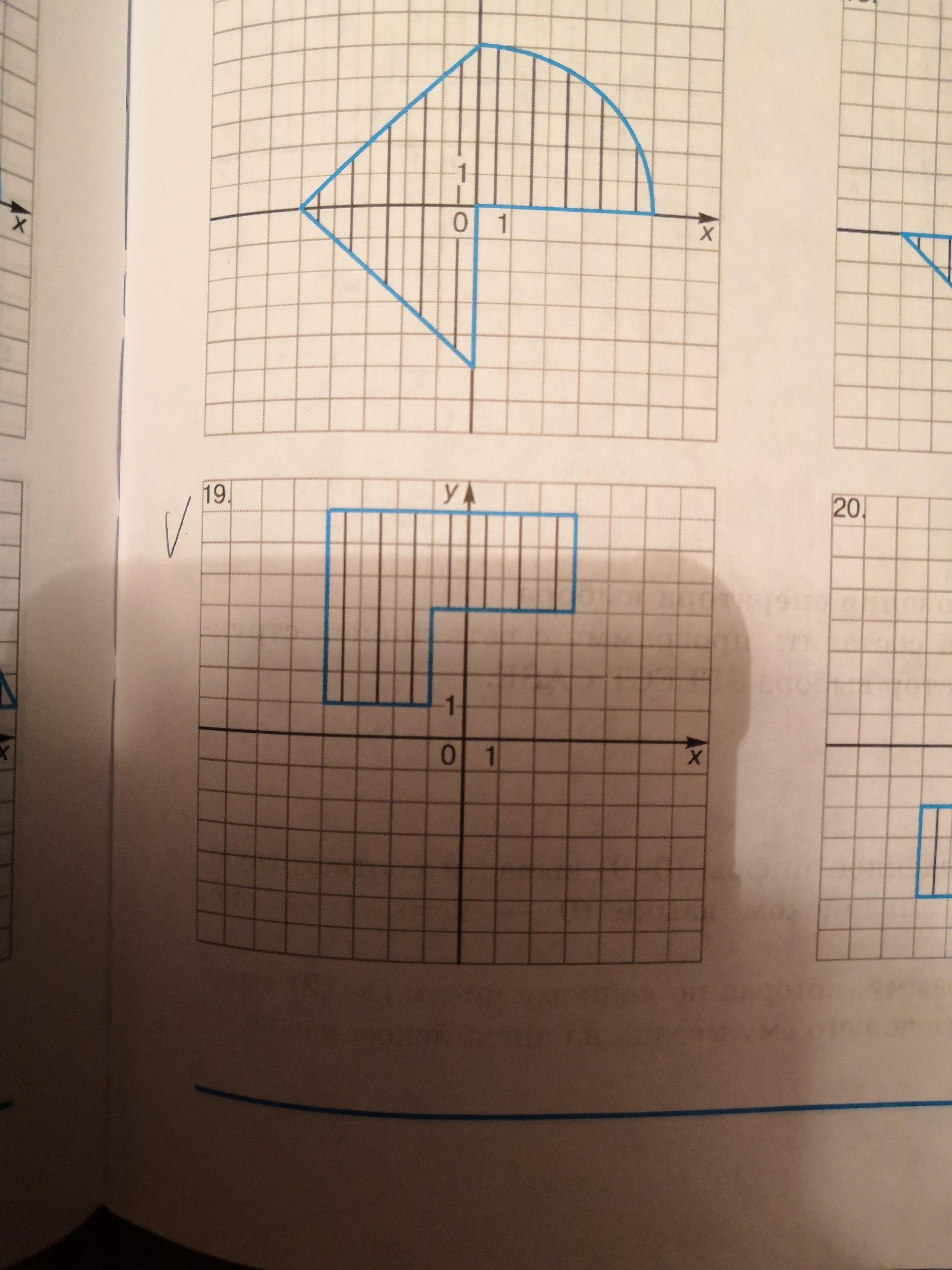
8. Дана точка А(х, у). Определить, принадлежит ли она прямоугольнику с вершинам в точках (х1, у1), (х2, у2) (х3, у3), (х4, у4). (прикреплю фото2)

1. Длина окружности (L) и площадь круга (A) с радиусом R могут быть вычислены следующим образом:

Формула для длины окружности:

L = 2 π R

Формула для площади круга:

A = π R^2

Где π (пи) является математической константой, приближенно равной 3.14159.

Пример:

Пусть R = 5. Тогда для вычисления длины окружности и площади круга:

L = 2 3.14159 5 = 31.4159

A = 3.14159 5^2 = 78.53975

Таким образом, длина окружности с радиусом 5 равна 31.4159, а площадь круга с радиусом 5 равна 78.53975.

2. Площадь (A) и периметр (P) правильного N-угольника, описанного около окружности с радиусом R, могут быть вычислены следующим образом:

Формула для площади правильного N-угольника:

A = (N R^2 sin(360/N)) / 2

Формула для периметра правильного N-угольника:

P = N R sin(180/N)

Где sin(x) - значение синуса угла x, N - количество сторон угольника.

Пример:

Пусть N = 6 и R = 4. Тогда для вычисления площади и периметра:

A = (6 4^2 sin(360/6)) / 2 = 41.5692

P = 6 4 sin(180/6) = 24

Таким образом, площадь правильного шестиугольника описанного около окружности с радиусом 4 равна 41.5692, а периметр равен 24.