-
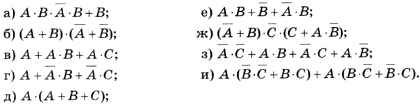
Упростите логические выражения с развернутым ответом и решением
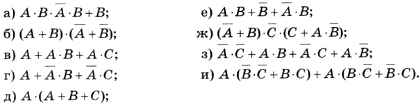
-
Предмет:
Информатика -
Автор:
t50_v.n.varlamov - 3 года назад
-
Ответы 1
-
Пример 1.
Пусть нам необходимо упростить логическое выражение:
(А &. В) + (A & ¬В).
1.Воспользуемся правилом дистрибутивности и вынесем за скобки А:
(А & В) + (А & ¬В) = А & (В + ¬В).
2.По закону исключенного третьего В + ¬В = 1, следовательно:
А & (В + ¬B) = А & 1 = А.
Пример 2.
Пусть нам необходимо упростить логическое выражение:
¬(A +¬B)+¬(A+ B)+ A & B
1. сначала раскрываем инверсию сложных выражений, используя законы де Моргана:
¬(A +¬B)+¬(A+ B)+ A & B=¬A&B + ¬A&¬B + A& B
2. выносим за скобки в первых двух слагаемых и используем закон исключения третьего
В + ¬В = 1:
¬A&B + ¬A&¬B + A& B=¬A&(B+¬B)+A&B=¬A+A&B
3. наконец, применяем распределительный закон для операции «И» и еще раз закон исключения третьего A+ ¬A = 1, следовательно:
¬A+A&B=(¬A+A)&(¬A+B)=¬A+B
Пример 3.
Пусть нам необходимо упростить логическое выражение:
(А + В) & (А + С).
1)Раскроем скобки: (А + В) & (А + С) = A & A + A & C + B & A + B & C;
2)Так как A & A =A, следовательно,
A & A + A & C + B & A + B & C = A + A & C + B & A + B & C;
3)В высказываниях А и А & C вынесем за скобки А и используя свойство А + 1= 1, получим
A + A & C + B & A + B & C = A & (1 + C) + B & A + B & C = A + B & A + B & C;
4) Аналогично предыдущему пункту вынесем за скобки высказывание А.
A + B & A + B & C = A & (1 + B) + B & C = A + B & C.
-
Автор:
Fedoseewa27 - 2 года назад
-
0
-
-
Добавить свой ответ
- Помогите пожалуйста решить задачу По геометрии 8 класс
-
Физика 9 класс пожалуйста нужен рисунок
-
Предмет:
Физика -
Автор:
daffodil6o2n - 3 года назад
-
Ответов:
2 -
Смотреть
-
- Решите уравнение -0,2(x-8)=0,4(x-3)
-
Информатика или геомтрия
-
Предмет:
Геометрия -
Автор:
korbinwvi3 - 3 года назад
-
Ответов:
1 -
Смотреть
-
