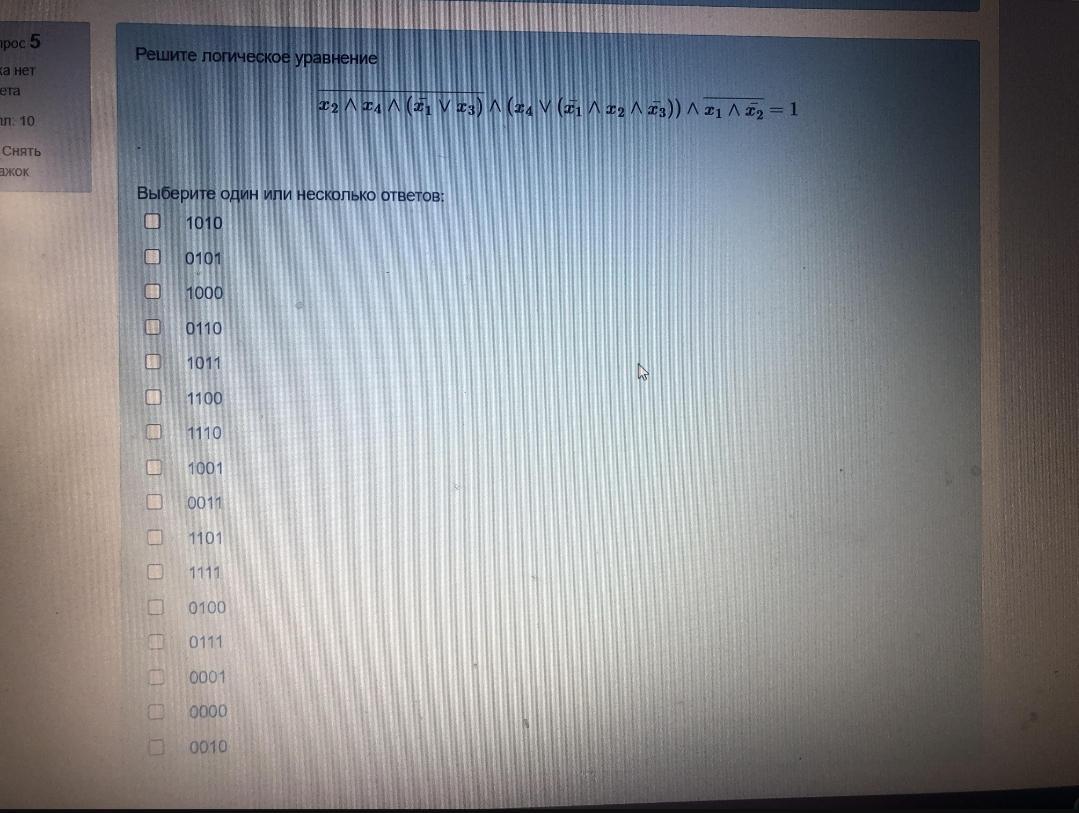
Решите логическое уравнение ¬(x2∧x4∧(¬x1∨x3))∧(x4∨(¬x1∧x2∧¬x3))∧¬(x1∧x2)=1 И выберите 1 или несколько вариантов ответа

Для решения данного уравнения следует использовать теоремы де Моргана, законы дистрибутивности и ассоциативности логических операций.

1. ¬(x2∧x4∧(¬x1∨x3)) = (¬x2∨¬x4∨(x1∧¬x3))

2. x4∨(¬x1∧x2∧¬x3) = (x4∨¬x1)∧(x4∨x2)∧(x4∨¬x3)

3. ¬(x1∧x2) = ¬x1∨¬x2

Подставим эти выражения в исходное уравнение:

(¬x2∨¬x4∨(x1∧¬x3))∧((x4∨¬x1)∧(x4∨x2)∧(x4∨¬x3))∧(¬x1∨¬x2) = 1

Разобьем это уравнение на три подуравнения и решим их по отдельности.

1. ¬x2∨¬x4∨(x1∧¬x3) = 1

Выполним дополнение до конъюнкции:

¬(¬x2∨¬x4∨(x1∧¬x3)) = 0

(x2∧x4∧(¬x1∨x3)) = 0

x2=0 или x4=0 или (¬x1∨x3)=0

x2=0 или x4=0 или (x1=1 и x3=1)

2. (x4∨¬x1)∧(x4∨x2)∧(x4∨¬x3) = 1

Конъюнкция равносильна тому, что все ее элементы равны 1:

x4=1 или x2=1 или x1=0 и x3=0

3. ¬x1∨¬x2 = 1

Конъюнкция равносильна тому, что оба ее элемента равны 0:

x1=1 и x2=1

Таким образом, исходное уравнение имеет два решения:

1. x2=0, x4=0, x1=1, x3=1

2. x2=1, x4=1, x1=0, x3=0

Ответ: (б) 2 решения.