-
№1
Сколько корней уравнения принадлежат промежутку[π/6;5π/6]:
(cos3 x+cosx)/(1-sinx )=0
№2
Решить неравенства:
а) 2 cos( x+π/3)<√3;
б) tg(π/4-2x)>1
№3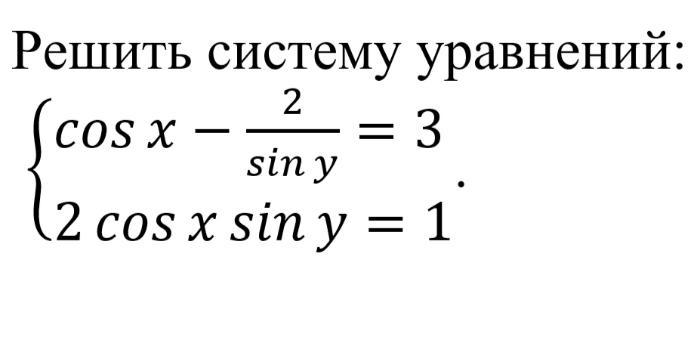
-
Предмет:
Литература -
Автор:
charlottefoster - 6 лет назад
-
Ответы 1
-
Ответ:
номер 1
Объяснение:
2sin(2x+(π/6))=2·sin2x·cos(π/6)+2cos2x·sin(π/6)=√3sin2x+cos2x;
√3sin2x+cos2x–cosx=√3sin2x–1;
cos2x–cosx+1=0
cos2x–sin2x–cosx+sin2x+cos2x=0
2cos2x–cosx=0
cosx·(2cosx–1)=0
cosx=0 ⇒ x= (π/2)+πk, k ∈ Z
Указанному промежутку принадлежит
х=(π/2)+3π=(7π/2)
(5π/2)< (7π/2) < 4π
2cosx–1=0
cosx=1/2
x= ± arccos(1/2)+2πn, n ∈ Z
x= ± (π/3)+2πn, n ∈ Z
Указанному промежутку принадлежат корни:
х=(–π/3)+4π=11π/3
(5π/2) < (11π/3) < 4π
О т в е т. (π/2)+πk, k ∈ Z; ± (π/3)+2πn, n ∈ Z
б) (7π/2); (11π/3)
-
Автор:
arrow - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Укажите сколько решений имеет система уравнений {-8x-6y=20 4x+3y=10
-
Предмет:
Алгебра -
Автор:
scoutjarvis - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
2144. Запиши решение задачи в виде одного
выражения Бычисли и запиши ответ задачи.
в двух бочках 60 л воды, когда в первую бочку
долили ещё 10 л в бочках воды стало поровну.
сколько литров воды было сначала в первой бочке?
90
-
Предмет:
Математика -
Автор:
brandivasquez - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
В первом мешке в 2 раза больше муки, чем во втором. После того, как со второго мешка отсыпали 5 кг в первый, во втором стало в 3 раза меньше, чем первом. Сколько кг муки было в каждом мешке сначала.
-
Предмет:
Математика -
Автор:
lefty - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Определите силу тяжести которую оказывает брусок чугуна размерами 8*9*7.Плотность чугуна 7000кг\м3.(Полное решение и условие)
How much to ban the user?
1 hour
1 day
100 years
