Найти интервал сходимости степенного ряда и исследовать его на концах

Найти интервал сходимости степенного ряда и исследовать его на концах
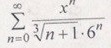
- Предмет:
  Математика
- Автор:
  victoralexander
- 5 лет назад

Ответы 1

$a_n= \frac{1}{ \sqrt[3]{n+1} \cdot6 ^{n} }$ тогда $a_{n+1}= \frac{1}{ \sqrt[3]{(n+1)+1} \cdot6 ^{n+1} }$ $R= \lim_{n \to \infty} \frac{a_n}{a_{n+1}}= \lim_{n \to \infty} \frac{ \frac{1}{ \sqrt[3]{n+1} \cdot 6 ^{n}} }{ \frac{1}{ \sqrt[3]{n+2} \cdot6 ^{n+1} }}=6$ Интервал сходимости (-6;6)При х=-6Получим знакочередующийся ряд, который сходится по признаку ЛейбницаПри х=6 ряд расходится по интегральному признаку.
- Автор:
  sonny1e6y
- 5 лет назад
- 0
Добавить свой ответ

Еще вопросы

Помогите!!!!!!
Ex. 47. Use Present Simple or Past Simple of the verbs in
brackets.
1. A: (hear, you) … the thunder last night? B: No, I … . I (hear,
not) … anything all night. I (be) … asleep. 2. A: Listen! (hear, you) …
a siren in the distance? B: No, I (not) … . I (hear, not) … anything at
all. 3. A: (build, you) … that bookshelf? B: No, I … . My uncle (build)
… it for me. 4. A: (be, a fish) … slippery to hold? B: Yes, … . It can
slip right out of your hand. A: How about frogs? (be, they) … slippery? B: Yes, … . A: What about snakes? B: I (know, not) … . I’ve
never touched a snake. 5. A: I (want) … to go to the mall this afternoon and (look) … for a new bathing suit. (want, you) … to go with
me? B: I can’t. I (have) … an appointment with my English teacher.
Besides, I (buy) … a new bathing suit last year. I (need, not) … a new one this year. 6. I (offer) … to help my older neighbor carry her groceries into her house every time I see her return from the store. She
(be) … always very grateful. Yesterday, she (offer) … to pay me for
helping her, but of course I (accept, not) … the offer. 7. Last Monday
night, I (take) … my sister and her husband to my favorite restaurant
for dinner and (find) … the doors locked. I (know, not) … it then, but
my favorite restaurant (be, not open) … on Mondays. We (want, not)
… to eat anywhere else, so we (go) … back to my house. I (make) … a
salad and (heat) … some soup. Everyone (seem) … satisfied even
though I (be, not) … a wonderful cook. 8. My daughter is twenty-one
years old. She (like) … to travel. My wife and I (worry) … about her a
little when she (be) … away from home, but we also (trust) … her
judgement. Last year, after she (graduate) … from the college, she
(go) … to Europe with two of her friends. They (travel, not) … by
train or by car. Instead, they (rent) … motor scooters and slowly
(ride) … through each country they visited. While she (be) … away,
my wife and I (worry) … about her safety. We (be) … very happy when
we (see) … her smiling face at the airport and (know) … that she was
finally safe at home.
- Предмет:
  Английский язык
- Автор:
  ducky6nio
- 5 лет назад
- Ответов:
  
  1
- Смотреть
гидроксосульфид кальция и дигидроксосульфат алюминия формула и структурная формула
- Предмет:
  Химия
- Автор:
  geraldzd9j
- 5 лет назад
- Ответов:
  
  1
- Смотреть
Напишите программу, которая в последовательности целых чисел вычисляет сумму всех чисел, кратных 5 или 9. Программа получает на вход целые числа, количество введенных чисел неизвестно, последовательность чисел заканчивается числом 0 (0 - признак окончания ввода, не входит в последовательность). Количество чисел не превышает 1000. Введенные числа по модулю не превышают 30 000. Программа должна вывести одно число: сумму всех чисел, кратных 5 или 9.
- Предмет:
  Информатика
- Автор:
  jamesoncross
- 5 лет назад
- Ответов:
  
  1
- Смотреть
сообшенее о животных из красной книги

спасобо (за ранее) :)
- Предмет:
  Другие предметы
- Автор:
  ana32
- 5 лет назад
- Ответов:
  
  2
- Смотреть

Найти интервал сходимости степенного ряда и исследовать его на концах

Ответы 1

Топ пользователей