-
ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА
Решите неравенства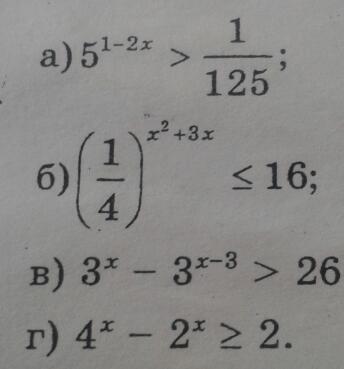
-
Предмет:
Математика -
Автор:
bandit67 - 6 лет назад
-
Ответы 1
-
а)5^(1-2x)>1\1255^(1-2x)>5^(-3)1-2x>-3-2x>-4 при делении на отрицательное число знак неравенства меняетсяx<2б)(1/4)^(x²+3x)≤164^(-(x²+3x)≤4²-x²-3x≤2x²+3x+2≤0 x²+3x+2=0 D=9-4·2=1 x1=(-3+1)\2=-1 x2=-2на числовой прямой отмечаем точки -1 и -2 ( закрашенные)х∈[-1 ; -2 ]в)3^x -3^(x-3)>263^x-3^x·3^(-3)>2627·3^x-3^x>26·2726·3^x>26·3³3^x>3³x>3г)4^x-2^x>22^(2x)-2^x-2>0Введём замену переменной , пусть 2^x=yy²-y-2>0 y²-y-2=0 D=1-4·(-2)=9 y1=(1+3)\2=2 y2=-1Возвращаемся к замене: 2^x=y12^x=2x=1 2^x=-1 корней нетна числовой прямой наносим число 1 ( пустое, не входит в множество решений) , при подстановки в неравенство чисел меньше 1 и больше 1 имеем ответ : х∈(1;∞)
-
Автор:
joenp5u - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Как решить пример 1803 * 2600
-
Предмет:
Математика -
Автор:
amber16 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
небылицы очень нужно
-
Предмет:
Другие предметы -
Автор:
dariennvc8 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
помогите прибаветь к словам турист и сосед прибавить суффикс -ск-
-
Предмет:
Русский язык -
Автор:
micaelatkt6 - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
добавить слог чтобы получилось слово с мягким знаком(жу_)
-
Предмет:
Русский язык -
Автор:
ashlynvc41 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
