-
Помогите, пожалуйста, решить уравнение под цифрой 3. Если можно с проверкой. Заранее спасибо.
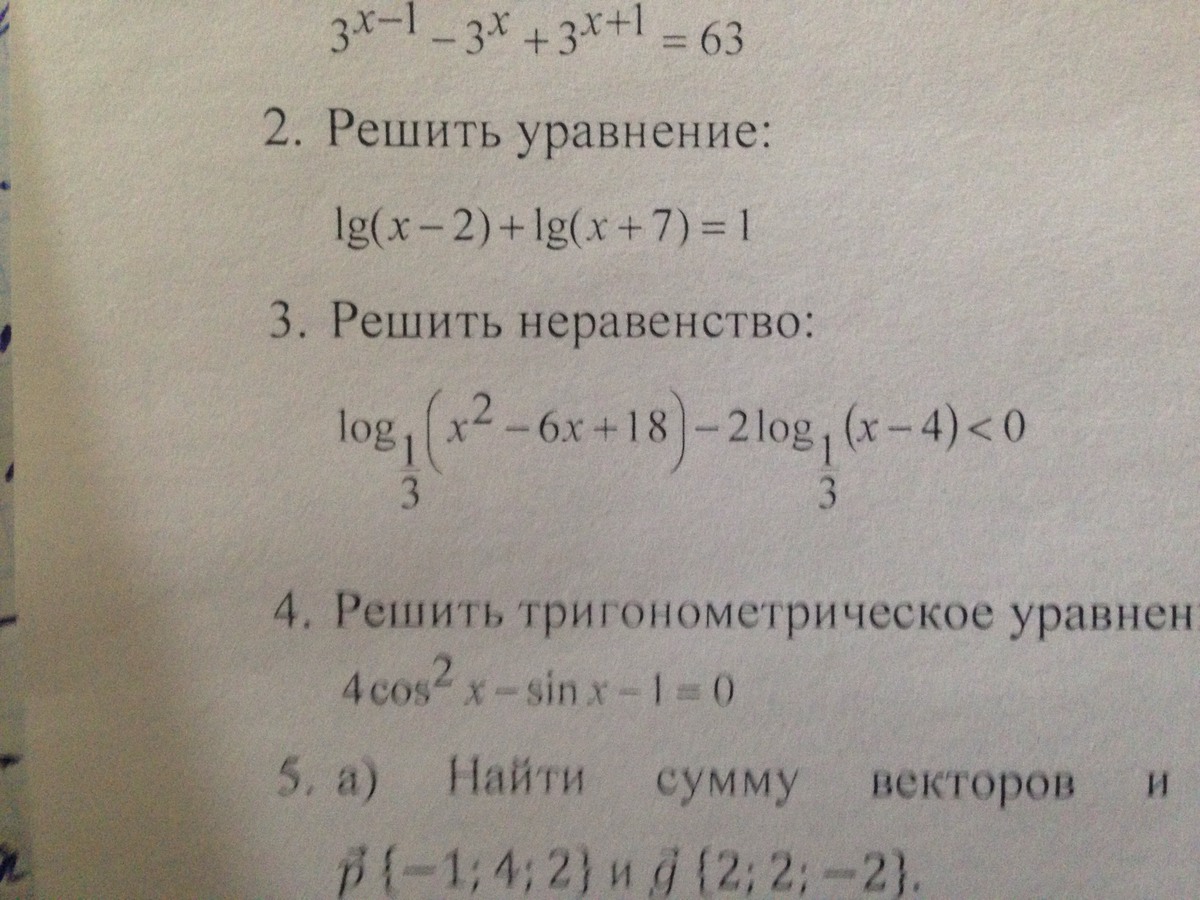
-
Предмет:
Математика -
Автор:
boyer - 6 лет назад
-
Ответы 1
-
3.log₁/₃ (x²-6x+18) - 2 log₁/₃ (x-4) <0log₁/₃ (x²-6x+18) - log₁/₃ (x-4)² <0log₁/₃ [(x²-6x+18)/(x-4)²] < log₁/₃ 1{x²-6x+18>0{x-4>0{ x²-6x+18 > 1 (x-4)²1) x²-6x+18>0Парабола, ветви вверх.х²-6х+18=0Д=36-72=-36 <0парабола не пересекает ось ОХ.парабола лежит выше оси ОХ.х²-6х+18>0 при любых Х.х∈(-∞; +∞)2) х-4>0 x>43) x²-6x+18 > 1 (x-4)²x²-6x+18 - 1 >0 (x-4)²x²-6x+18-(x-4)² >0 (x-4)²x²-6x+18-x²+8x-16 >0 (x-4)²2x+2 >0 (x-4)²2(x+1) >0 (x-4)²(x+1)(x-4)(x-4)>0x=-1 x=4 - + +------- -1 ------- 4 --------------- \\\\\\ \\\\\\\\\\\\\\\x∈(-1; 4)U(4; +∞)В итоге имеем:{x∈(-∞; +∞){x>4{x∈(-1; 4)U(4; +∞)Отсюда:х>4Проверка:х=5 >4log₁/₃ (5²-6*5+18) - 2log₁/₃ (5-4) <0log₁/₃ (25-30+18) - 2log₁/₃ 1 <0log₁/₃ 13 -2*0 <0log₁/₃ 13 <0-2,33 <0Ответ: х>4
-
Автор:
blackiehamilton - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
В чём мораль сказки "Шемякин суд"?
-
Предмет:
Литература -
Автор:
moonshineaqjg - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Какое изменение в строении стопы появилось у человека в связи с прямохождением?
1) Срослись кости предплюсны.
2) Сформировались своды.
3) В большом пальце появились две фаланги.
4) Большой палец приобрёл подвижность.-
Предмет:
Биология -
Автор:
roberto859 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
вознеси в процентах число 1/5.
-
Предмет:
Алгебра -
Автор:
karlibooker - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Пропилацетат образуется при взаимодействии
1) ацетилена и воды
2) этановой кислоты и пропанола
3) метанола и этанола
4) уксусной кислоты и этанола
-
Предмет:
Химия -
Автор:
gonzálezyv5o - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
