Задать вопрос Регистрация
Помочь другим

  • 52/(3^(3-x^2)-1)^2-28/(3^(3-x^2)-1)+1
    Решал это неравенство на ЕГЭ, по моему решил правильно, но баллы за неё не дали.
    Решите пожалуйста этот пример чтобы я сверил ответ со своим. Спасибо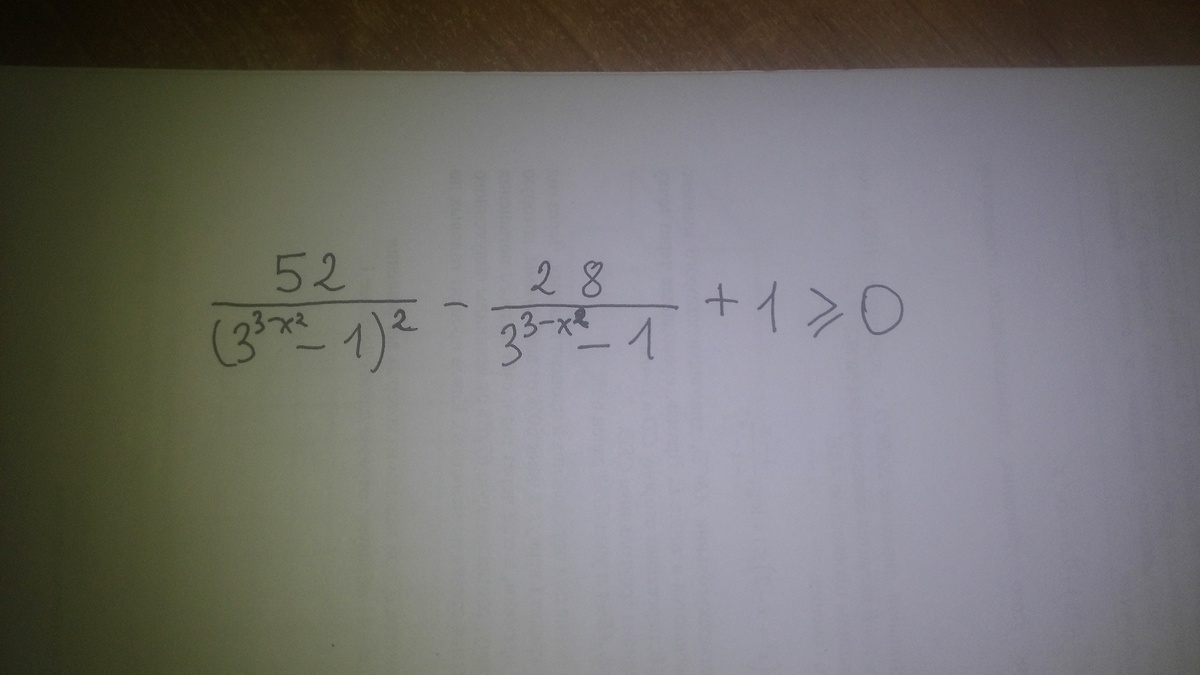

    question img

Ответы 1

  • \frac{52}{( 3^{3- x^{2} } -1)^2} - \frac{28}{3^{3- x^{2} } -1} +1 \geq 0ОДЗ:   3^{3- x^{2} } eq 0x eq \sqrt{3 x eq - \sqrt{3} введем замену [tex]3^{3- x^{2} } -1 \leq 2  =a[/tex] \frac{52}{a^2} - \frac{28}{a} +1 \geq 0 \frac{a^2-28a+52}{a^2} \geq 0D=784-208=576a1=26a2= 2 \frac{(a-26)(a-2)}{a^2} \geq 0решаем методом интервалов и получаемa \leq 2 a \geq 263^{3- x^{2} } -1 \geq 263^{3- x^{2} } \leq 33^{3- x^{2} } \geq 273- x^{2} \leq 13- x^{2} \geq 3- x^{2} \leq -2- x^{2} \geq 0 x^{2} -2 \geq 0 x^{2} \leq 0        x=0 в пересечении с ОДЗ  получаем Ответ: ( - ∞; √3) (√3; √2] {0} [√2;√3) (√3; + ∞)

    • Автор:

      zhang
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years