-
Найти значения параметра a, для каждого из которых неравенство, верно при всех значениях x, задача изложена в изображении
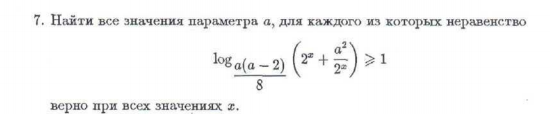
-
Предмет:
Математика -
Автор:
andycarpenter - 6 лет назад
-
Ответы 1
-
1) Если основание логарифма0 < a(a - 2)/8 < 10 < a^2 - 2a < 8{ a(a - 2) > 0{ a^2 - 2a - 8 = (a - 4)(a + 2) < 0Получается{ a < 0 U a > 2{ a < -2 U a > 4Область определения: a < -2 U a > 4 При этом функция логарифма - убывающая. Тогда2^x + a^2/2^x <= a(a - 2)/8Замена 2^x = y > 0 при любом хy + a^2/y - a(a - 2)/8 <= 0(8y^2 - a(a - 2)*y + 8a^2) / y <= 0y > 0 при любом х, поэтому8y^2 - (a^2 - 2a)*y + 8a^2 <= 0Это неравенство не может быть верно при любом y, только на отрезке (y1; y2)Значит, если 0 < a(a - 2)/8 < 1, то решений нет.2) Если основаниеa(a - 2)/8 > 1a^2 - 2a > 8a^2 - 2a - 8 > 0(a - 4)(a + 2) > 0Область определения: a < -2 U a > 4При этом функция логарифма - возрастающая. Тогда2^x + a^2/2^x >= a(a - 2)/8Замена 2^x = y > 0 при любом х y + a^2/y - a(a - 2)/8 >= 08y^2 - (a^2 - 2a)*y + 8a^2 >= 0D = (a^2 - 2a)^2 - 4*8*8a^2 = a^4 - 4a^3 + 4a^2 - 256a^2 = a^4 - 4a^3 - 252a^2Если это верно при любом х (и при любом у), то D < 0 a^4 - 4a^3 - 252a^2 < 0Делим все на a^2 > 0a^2 - 4a - 252 < 0D/4 = 4 + 252 = 256 = 16^2a1 = 2 - 16 = -14; a2 = 2 + 16 = 18Решение: (-14, 18)С учетом области определения: a < -2 U a > 4Ответ: (-14; -2) U (4; 18)
-
Автор:
reinaldobarber - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
первое пропорцией называется а что дальше и второе их данных отношений выберите те из которых можно составить пропорции .И 3 числа.Цифры 2,4:0,8
6,4:1,6-
Предмет:
Математика -
Автор:
beaubrooks - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Замени в предложениях глаголы в прошедшем времени глаголами настоящего времени.
Сначала землю пахали: шёл трактор по полю и тянул за собой плуг. Потом землю боронили: разбивали плотные комки земли и выравнивали почву. Вёл борону по полю тоже трактор. Теперь почва готова к посеву. К трактору прицепил сеялку. Сеялка засыпала в землю семена . Зерно прорастало . Вот появился зелёный стебелёк.
СРОЧНО дам 30 баллов!-
Предмет:
Русский язык -
Автор:
scooby - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Описание героини Ассоль из Алых парусов
Спасибо)-
Предмет:
Литература -
Автор:
mcclain - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
морфологический разбор слова : чуть-чуть
-
Предмет:
Русский язык -
Автор:
guzmán89 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
