Задать вопрос Регистрация
Помочь другим

  • Как решаются такие примеры ?с подробным решением пожалуйста

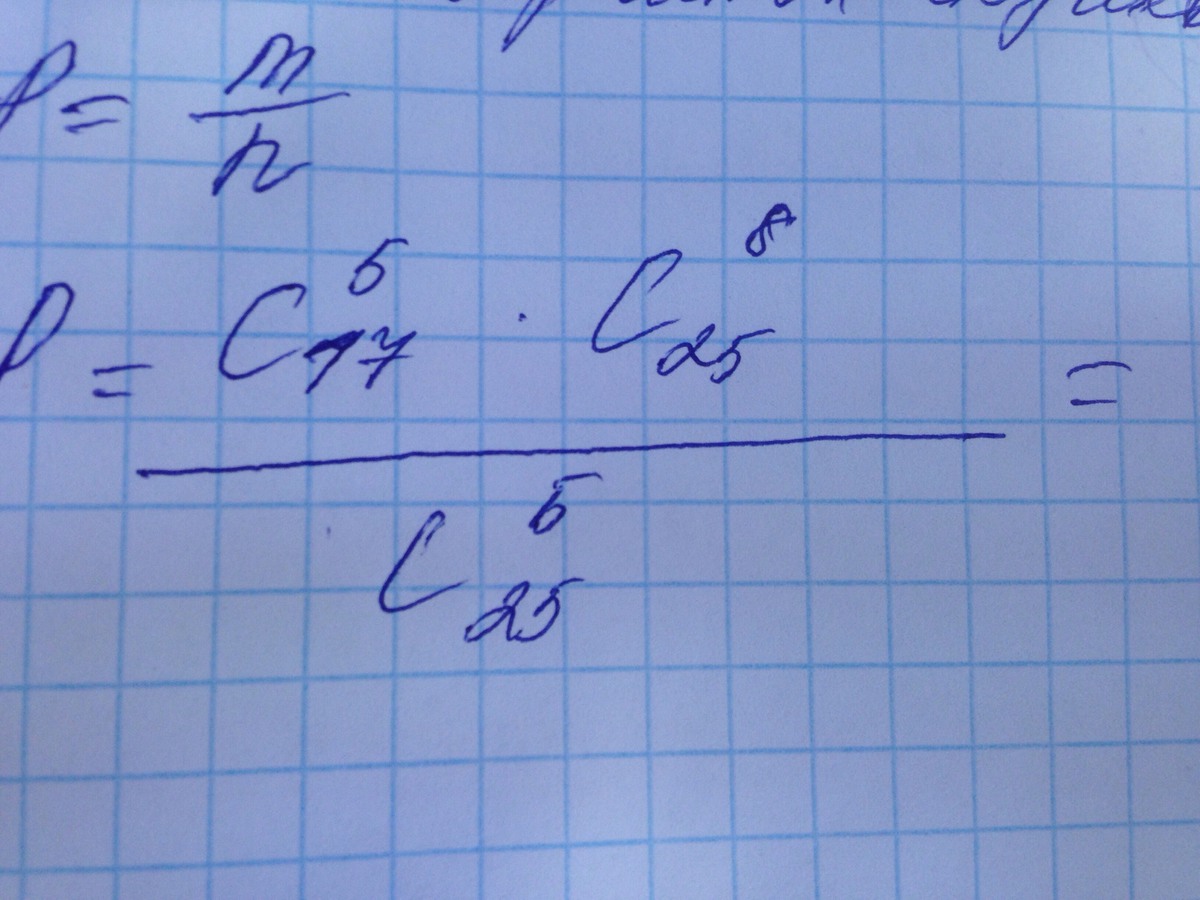
    question img

Ответы 4

  • от куда 20 берется ?
  • 20! из знаменателя сочетания 25 5 в знаменателе переходит в числитель

  • Это называется сочетания. Они вычисляются по формуле (см картинку начиная с С). Каждое С в примере заменяем на эту формулу и все под одну дробь:

    Пример=17!*25!*5!*20!-------5!*12!*8!*17!*25!=125970  (-----черта дроби)

    Ответ:125970

    answer img
  • C^k_n=\frac{n!}{k! \cdot (n-k)!}; \\\\ n!=1 \cdot 2 \cdot 3 \cdot... \cdot n; \ \ k! = 1 \cdot 2 \cdot 3 \cdot ... \cdot k \\ \\ C^5_{17}=\frac{17!}{5! \cdot (17-5)!}=\frac{17!}{5! \cdot 12!}=\frac{1 \cdot 2 \cdot 3 \cdot .. . \cdot 12 \cdot 13 \cdot 14 \cdot 15 \cdot 16 \cdot 17}{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 1 \cdot 2 \cdot 3 \cdot ... \cdot 12}=\frac{13 \cdot 14 \cdot 15 \cdot 16 \cdot 17}{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 }= \\ \\ =13 \cdot 7  \cdot 4 \cdot 17 =6188\\ \\ C^8_{25}=\frac{25!}{8! \cdot (25-8)!}=\frac{25!}{8! \cdot 17!}=\frac{18 \cdot 19 \cdot 20 \cdot 21 \cdot 22 \cdot 23 \cdot 24 \cdot 25}{2\cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8}=3 \cdot 19 \cdot 3 \cdot 11 \cdot 23 \cdot 25=\\ \\ = 1081575 \\ \\ C^5_{25}=\frac{25!}{5! \cdot (25-5)!}=\frac{25!}{5! \cdot 20!}=\frac{21 \cdot 22 \cdot 23 \cdot 24 \cdot 25}{2 \cdot 3 \cdot 4 \cdot 5}=7 \cdot 11 \cdot 23 \cdot 6 \cdot 5=53130Проверьте первоначальную формулы вероятности, иначе получается... (сочетания посчитаны верно)\\ \\ P=\frac{C^5_{17} \cdot C^8_{25}}{C^5_{25}}=\frac{6188 \cdot 1081575}{53130}=125970
    answer img

    • Автор:

      darius79
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years