-
Помогите решить систему неравенств
{(x≥(2x+18)/(x-1)
{log_2 (1+x) ≤ 3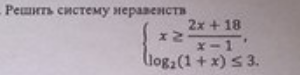
-
Предмет:
Математика -
Автор:
tristenjee2 - 6 лет назад
-
Ответы 3
-
Спасибо очень помогла
-
Автор:
browniehicks - 6 лет назад
-
0
-
-
Пожалуйста!) обновите страничку только
-
Автор:
emmanuelyrkg - 6 лет назад
-
0
-
-
Решаем по очереди каждое неравенство, а затем объединяем решения:1 неравенство:
_____-_____
_____+_____
_____-______
_____+_____1)
2 неравенство:
ОДЗ:
Решение:
одз: _______
____________________решение: __________________
_________2)
ОБЩЕЕ РЕШЕНИЕ:1) _______
________
________
_________
________2) ____________
______________________
________Ответ:
-
Автор:
friedman - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- установить соответствие между географической координатой и цифрой, которой она указана на карте:
-
1756 и 1791 напишите словами на английском
-
Предмет:
Английский язык -
Автор:
méndezspdd - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Сколько страниц в книге О. Генри "Дары волхвов и Вождь краснокожих"?
-
Предмет:
Литература -
Автор:
pruitt - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В уравнении электролитической диссоциации соли K2Mg(FeOH)(SO4)3 общее число ионов составляет 1) 5; 2) 6; 3) 7; 4) 4.
-
Предмет:
Химия -
Автор:
kaileeatuf - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
