-
Решите логарифмическое неравенство и укажите его наибольшее значение
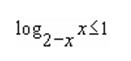
-
Предмет:
Математика -
Автор:
mulligank497 - 6 лет назад
-
Ответы 1
-
ОДЗ данного неравенства:{2-x>0{x>0{2-x≠1или {x<2{x>0{x≠1(0;1)U(1;2)Данное неравенство эквивалентно следующим неравенствам{x>0 {x>0{2-x>1 ⇔ {x<1{x ≤ 2-x {x≤1Решение данной системы неравенств является интервал (0;1)и{x>0 {x>0{0<2-x<1 ⇔ {1<x<2 {x≥2-x {x≥1Решением данной системы неравенств является интервал(1;2)Поэтому исходное неравенство имеет решения для всех значений х ∈(0;1)U(1;2)Ответ:(0;1)U(1;2)Легко доказать что исходное неравенство истинно на всей области его определения или что
для всехзначений х ∈(0;1)U(1;2) так как
В данной дроби числитель при значении х∈(0;1) отрицателен, а при значении х∈(1;2) положителен.Знаменатель наоборот при при значении х∈(0;1) положителен, а при значении х∈(1;2) отрицателен. Поэтому значение дроби для всех значений х∈(0;1)U(1;2) всегда меньше нуля. Раз данный логарифм при всех значениях х∈(0;1)U(1;2) меньше нуля то следовательно и меньше 1.Наибольшего целого значения решения неравенства нет.
-
Автор:
kristian - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
на координатной плоскости изображён график квадратичной функции. Найдите разность между значением данной функции в точке -6 и значением данной функции в точке -1
-
Предмет:
Алгебра -
Автор:
julianyg19 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Всем привет! Заинтересовался одной задачей, решения в интернете НЕТ. Поэтому, если вы знаете, как её решить - решите, только, пожалуйста, объясните, как вы это сделали. Если вы не знаете, как её решать - не решайте. Хочу увидеть чёткий, адекватный ответ. Спасибо! Вот сама задача (кстати, не уверен, что её вообще можно решить, поэтому не обольщайтесь). Тема: комбинаторика.
Задача достаточно короткая: Для вычислительной машины, способной просчитать миллион игровых комбинаций в секунду с отсевом заведомо неоптимальных ветвей, на просчёт 6 ходов вперёд потребуется 1 секунда, на 12 ходов — 11 дней, а на 18 ходов — около 32000 лет. Вопрос: сколько лет потребуется этой самой вычислительной машине на то, чтобы просчитать 70 ходов? (Задача очень даже правдоподобна, под "игровыми комбинациями" подразумеваются шахматные комбинации. Спасибо!-
Предмет:
Алгебра -
Автор:
cullenhebert - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
как вычислить квадратура 6 на 3
-
Предмет:
Математика -
Автор:
fatty - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
в каком варианте ответа выделенное слово употреблено неверно:1. вскоре новый жилец ОПЛАТИЛ все счета 2. Нам удалось ОГРАДИТЬ друга от несправедливых обвинений 3.Марью Николаевну ждала безрадостная ОДИНОЧНАЯ старость 4. В музее истории нашего города пройдет ПРАЗДНИЧНЫЙ концерт посвещенный ветеранам Великой Отечественной Войны
-
Предмет:
Русский язык -
Автор:
snugglestggw - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
