Задать вопрос Регистрация
Помочь другим

  • Написать уравнение касательной и нормали к графику функции

    Помогите пожалуйста очень нужно. в низу пример на скрине.

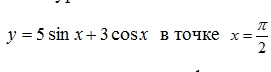
    question img

Ответы 1

  • y = 5sinx + 3 cosx\\ x_{0} = \frac{\pi}{2}

    уравнение касательной имеет общий вид

    (y - y_{0})=k*(x-x_{0})\\ y(= 5*cos\frac{\pi}{2}+ 3sin\frac{\pi}{2} = 5\\ (y - 5) =k*(x-x_{0})\\ k = y'(x_{0}) = 5cosx - 3sinx = 5cos\frac{\pi}{2} - 3sin\frac{\pi}{2} = -3\\ (y - 5) = -3(x-x_{0})\\ x_{0}=\frac{\pi}{2} \\ (y - 5) = -3(x-\frac{\pi}{2} )\\ y - 5 = -3x + \frac{3\pi}{2}\\ y = -3x + \frac{3\pi}{2}+5\\

    уравнение нормали к графику имеет схожий вид

    (y - y_{0})=-\frac{1}{k}(x-x_{0})\\

    значения нам уже известны, подставляем их

    (y - 5)=-\frac{1}{-3}(x-\frac{\pi}{2})\\ y - 5 = \frac{1}{3}x - \frac{\pi}{6}\\ y = \frac{x}{3} - \frac{\pi}{6} + 5

    в итоге уравнение касательной -  y = -3x + \frac{3\pi}{2}+5

    уравнение нормали y = \frac{x}{3} - \frac{\pi}{6} + 5

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years